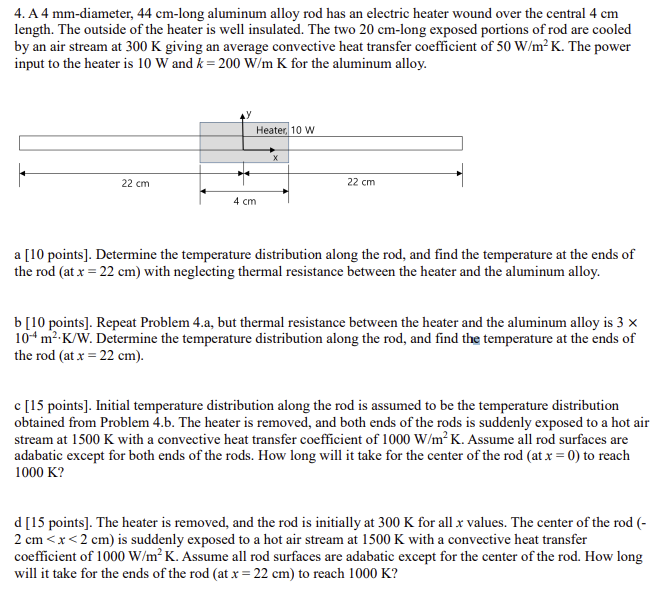
$4.$ A $4$ mm $-$diameter, $44$ cm $-$long aluminum alloy rod has an electric heater wound over the central $4$ cm length. The outside of the heater is well insulated. The two $20$ cm $-$long exposed portions of rod are cooled by an air stream at $300$ K giving an average convective heat transfer coefficient of $\backslash (50\backslash$mathrm$\{$~W$\}/\backslash$mathrm$\{$m$\}^\{2\}\backslash$mathrm$\{$~K$\}\backslash ).$ The power input to the heater is $10$ W and $\backslash ($ k$=200\backslash$mathrm$\{$~W$\}/\backslash$mathrm$\{$m$\}\backslash$mathrm$\{$K$\}\backslash )$ for the aluminum alloy.

a $[10$ points$].$ Determine the temperature distribution along the rod, and find the temperature at the ends of the rod $($at $\backslash ($ x$=22\backslash$mathrm$\{$~cm$\}\backslash ))$ with neglecting thermal resistance between the heater and the aluminum alloy.

b $[10$ points$].$ Repeat Problem $4.$a$,$ but thermal resistance between the heater and the aluminum alloy is $\backslash (3\backslash$times $\backslash )\backslash (10^\{-4\}\backslash$mathrm$\{$~m$\}^\{2\}\backslash$cdot $\backslash$mathrm$\{$~K$\}/\backslash$mathrm$\{$W$\}\backslash ).$ Determine the temperature distribution along the rod, and find the temperature at the ends of the $\backslash (\backslash$operatorname$\{$rod$\}(\backslash )$ at $\backslash ($ x$=22\backslash$mathrm$\{$~cm$\})\backslash ).$

c $[15$ points$].$ Initial temperature distribution along the rod is assumed to be the temperature distribution obtained from Problem $4.$b$.$ The heater is removed, and both ends of the rods is suddenly exposed to a hot air stream at $1500$ K with a convective heat transfer coefficient of $\backslash (1000\backslash$mathrm$\{$~W$\}/\backslash$mathrm$\{$m$\}^\{2\}\backslash$mathrm$\{$~K$\}\backslash ).$ Assume all rod surfaces are adabatic except for both ends of the rods. How long will it take for the center of the rod $($at $\backslash ($ x$=0\backslash ))$ to reach $1000$ K $?$

d $[15$ points$].$ The heater is removed, and the rod is initially at $300$ K for all $\backslash ($ x $\backslash )$ values. The center of the rod $(\backslash (2\backslash$mathrm$\{$~cm$\}$