Question: 4. Consider a distribution with probability density function f(x) and its mean is denoted by . The density is symmetric around at, i.e., f(u +y)

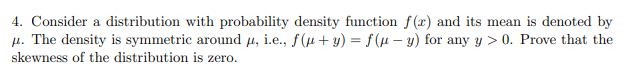
4. Consider a distribution with probability density function f(x) and its mean is denoted by . The density is symmetric around at, i.e., f(u +y) = f(u -y) for any y > 0. Prove that the skewness of the distribution is zero

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Question 1 Which of the following is not a characteristic of a probability density function f (x) ? A. f(x) 2 0 for all values of x. B. f (xx) is symmetric around the mean. C. The area under f (x)...

Practice Exam 1 1. (19 total points) PROBABILITY CALCULATIONS Let X be a continuous random variable with probability density function f (x) = 3x2 , for 0 x 1 . 2.0 1.0 0.0 f(x) = 3x2 3.0 Here is a...

Order Statistics. Let X 1 , X 2 , ¦. X n be a random sample of size n from X, a random variable having distribution function F(x). Rank the elements in order of increasing numerical magnitude,...

1. Let X be the number of tails in the experiment of tossing a balanced coin 4 times. Find the distribution of Y = - 1 1 +X 2. Let Xhas the Poisson distribution with probability distribution function...

Let X1, X2, .., An be a random sample from a distribution with probability density function In x 1 if 0 0; f (x0') = otherwise; Given: E (X) = : 2 ; and Var (1=]] -8. If f (x]o=) belongs to the...

&+ help here plss. 9. One-shot DMP model (inspired by Albrecht, Navaro and Vroman (2010]) Time: One period Demography: A unit mass continuum of workers and a larger mass of firms who can create...

(a) Fred visits Blotchville again. He finds that the city has installed an electronic display at the bus stop, showing the time when the previous bus arrived. The times between arrivals of buses are...

pease find solutions On a disc with origin (0, 0) and radius 1, a point (X, Y ) is selected by throwing a dart that hits the disc in an arbitrary place. This is best described by the joint...

complete all using simple calculations 1 Consider the following two random samples of ten observations which come from the distributions of random variables which assume non-negative integer values...

What quality characterizes the two main styles of thinking?

On January 1, 2008, Slidell Company received a 2-year, $500,000 loan, with interest payments occurring at the end of each year and the principal to be repaid on December 31, 2009. The interest rate...

13.43 Although we have not emphasized it, the paired t-test can be used to test hypotheses in which the null value is something other than 0. For example, suppose that the proponents of a diet plan...

Please analyse the net profit margin of Apple and BP according to the tables on the next page, then comment on why Apple's net profit margin of 26% is higher compared to BP's net profit margin of...

Do not go, wait until I come

Pay him, do not wait until I sign

Tell what you mean without sounding too dominant, i.e. show authority without sounding instructive