Question: 4. Define the sequence In as follows: given the initial value x1, find recursively Zn+1 = an+1 for n = 2, 3, .... Show that

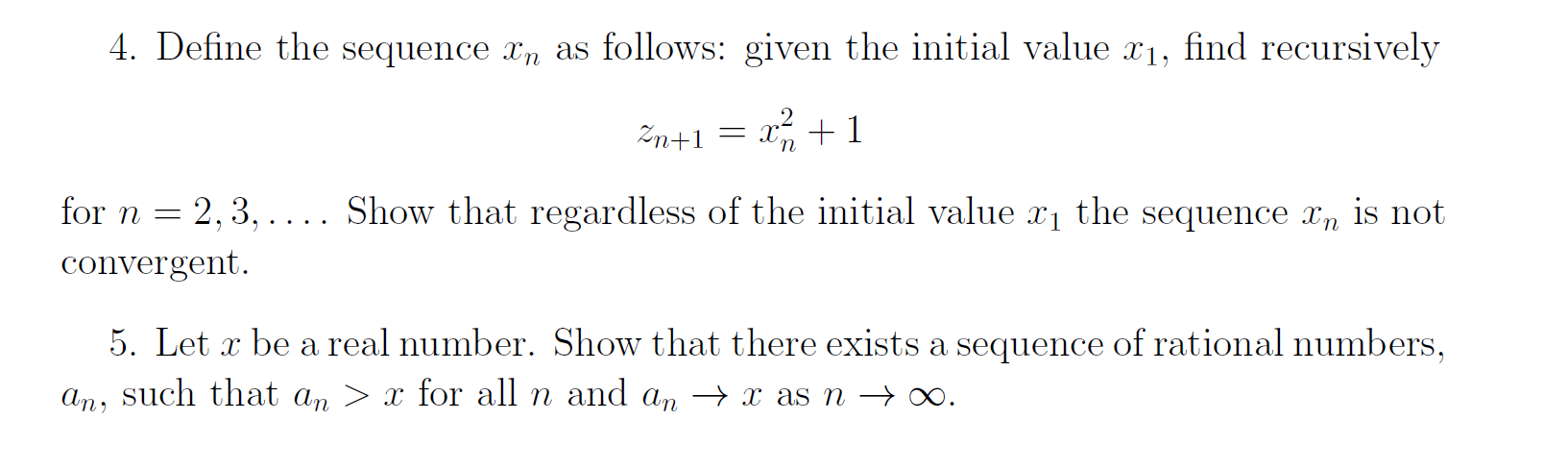
4. Define the sequence In as follows: given the initial value x1, find recursively Zn+1 = an+1 for n = 2, 3, .... Show that regardless of the initial value x, the sequence In is not convergent. 5. Let x be a real number. Show that there exists a sequence of rational numbers, an, such that an > x for all n and an > x as n - 0

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

exercise 4.3 Give the value process associated with the trading strategy (xt,yt)t=12 in Model 4.2, where (x1,y1)=(500,10),(x2(u),y2(u))=(227.27,15),(x2(d),y2(d))=(704.54,5), and show that this...

HW 12, MAT 312/AMS 351: SPRING 2017 Problem 1. (1) Set H = {4a + 6b | a, b Z} Z. Show that H is a subgroup of Z. (2) Is H cyclic? Problem 2. Write down all the cyclic subgroups of the following...

DETAILS What is the maximum segment length of a 100Base-FX netdwork, The last character ('X', etc) refers to the line code method used. Line code is a patdtern of voltage, current or photons used to...

1. A player throws a fair die and simultaneously flips a fair coin. If the coin lands heads, then she wins twice, and if tails, then one-half of the value that appears on the die. Determine her...

Give Correct ANSWERS Human-Computer Interaction (a) If you had been one of the original inventors of the WIMP interface, and engineers on the technical team had been sceptical about the advantages...

The Basics of Financial Mathematics Spring 2003 Richard F. Bass Department of Mathematics University of Connecticut c These notes are 2003 by Richard Bass. They may be used for personal use or class...

HW #8 (Fault Simulation) EE 623 1. Assume you have developed an efficient table-driven event-directed logic simulation system. Consider a fan-out free circuit C having n input lines, m output line, g...

MUST BE CORRECT ANSWERS A small software company has the following simplified cashflow, funded by shareholders' equity of 20,000 and a bank overdraft of 5000: Invoiced money received 2 months after...

1.2 A die is rolled repeatedly. Determine which of the following processes are Markov 1. The largest number Xn shown up to the n-th roll. 2. The number Nn of sixes in n rolls 3. At time n the time On...

In this question assume that p and q are atomic formulae. (a) Compare and contrast path formulae and state formulae in temporal logic. [4 marks] (b) Describe and contrast the meanings of F(G p) and...

Suppose you want to send your official name "Maharab Hossain Rakib" as a message from one computer to another computer. Now, find out the number of bits required to send your name using Huffman...

Assume Universal Accountancy services provide bookkeeping, tax, and audit services to its clients. Management believes the company has several unprofitable customers and would like to perform...

Concerning AAR: 1. Describe how the average accounting return is usually calculated and describe the information this measure provides about a sequence of cash flows. What is the AAR criterion...

Create a C# application named SalesTransactionDemo that declares several SalesTransaction objects and displays their values and their sum. The SalesTransaction class contains the following fields:...