Question: 4) Find the vertical position function, y(t), for the projectile. 5) When will the projectile hit the ground?7) If the current population of the town

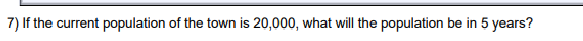
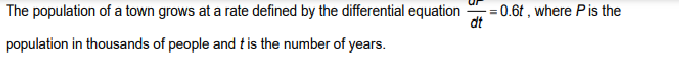
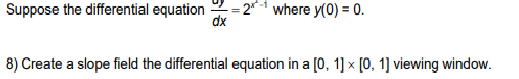



![differential equation in a [0, 1] x [0, 1] viewing window.9) Sketch](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6668435b3c824_0196668435b28619.jpg)



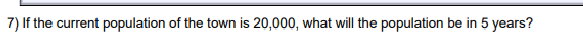
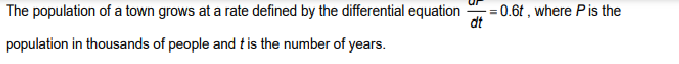



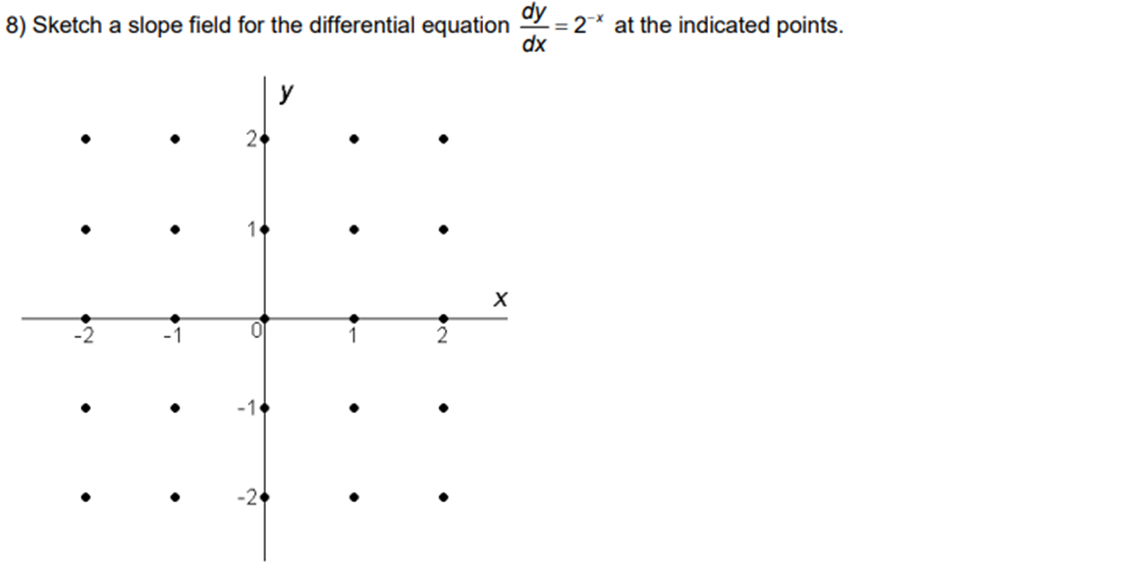


4) Find the vertical position function, y(t), for the projectile. 5) When will the projectile hit the ground?7) If the current population of the town is 20,000, what will the population be in 5 years?The population of a town grows at a rate defined by the differential equation 0.6t , where Pis the dt population in thousands of people and t is the number of years.Suppose the differential equation = 21 -1 dx where y(0) = 0. 8) Create a slope field the differential equation in a [0, 1] x [0, 1] viewing window.9) Sketch a solution curve that passes through the point representing the initial value.l 10) Use the solution curve through the initial value's point to approximate y(1) 7) Sketch a slope field for the differential equation dy = x' -2x at the indicated points. dx X -2 -18) Sketch a slope eld for the differential equation % = 2" at the indicated points. 9) A slope field is given for a particular differential equation. Sketch the solution that passes through the point (0, -1). X10) A slope field is given for a particular differential equation. Sketch the solution that passes through the origin. X 1-2 0 - 2 -1
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


