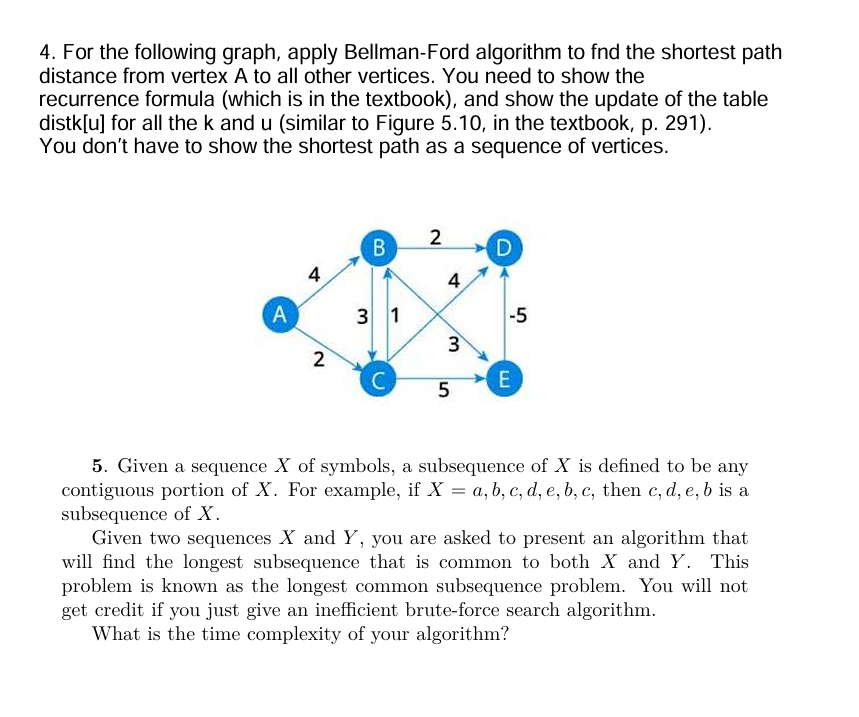
Question: 4 . For the following graph, apply Bellman - Ford algorithm to fnd the shortest path distance from vertex A to all other vertices. You
For the following graph, apply BellmanFord algorithm to fnd the shortest path distance from vertex A to all other vertices. You need to show the recurrence formula which is in the textbook and show the update of the table distku for all the k and u similar to Figure in the textbook, p You don't have to show the shortest path as a sequence of vertices.
Given a sequence X of symbols, a subsequence of X is defined to be any contiguous portion of X For example, if Xa b c d e b c then c d e b is a subsequence of X
Given two sequences X and Y you are asked to present an algorithm that will find the longest subsequence that is common to both X and Y This problem is known as the longest common subsequence problem. You will not get credit if you just give an inefficient bruteforce search algorithm.
What is the time complexity of your algorithm?
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


