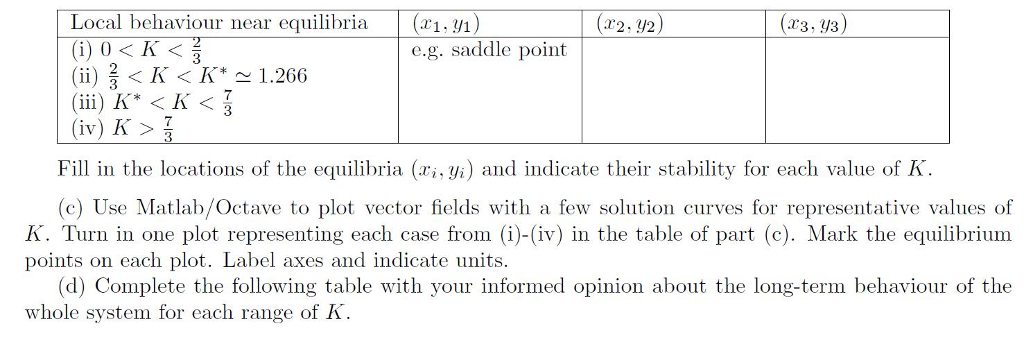
4. Improved predator prey model Let's make the model of the preceding question more realistic. First, let's replace the exponential growth of the prey with a logistic type growth, so a' (t) r(1 a in the absence of predators. We see that all solutions with initial conditions a (0) 0 tend to the equilibrium a K. We call I the carrying capacity of the prev habitat. Now let u be the population density of the predators and suppose that the predator population declines exponentially in the absence of prey, like y (t dy The previous question's model can be criticized because there is no limit to the rate of increase of the predator population or the rate of decline of the prey population. In reality, there is an upper limit on the rate at which prey can be caught and eaten by a predator. For this reason, ecological modellers are usually happier to use a "Holling Type II function for the per-capita predator consumption rate of prey. This function has the form p m reflecting the following features (1) p(0) 0 if no prey is present, then no predation occurs (2) p(ac) is an increasing function of a increasing prey population leads to an increase in prey consump tion by predators (3) p(ar) m as oo there is a maximum possible rate of prey consumption by predators even if prey are very abundant Putting this all together, we can write the whole improved model as: (1) (2) dy cm