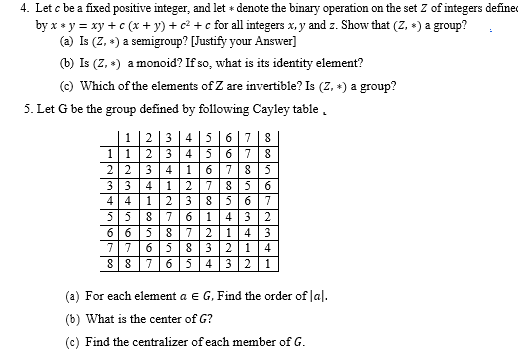
4. Let c be a fixed positive integer, and let * denote the binary operation on the set Z of integers define by x * y = xy + c (x + y) + c' + c for all integers x, y and z. Show that (Z, *) a group? () Is (Z. *) a semigroup? [Justify your Answer] (b) Is (Z, *) a monoid? If so, what is its identity element? (c) Which of the elements of Z are invertible? Is (Z, *) a group? 5. Let G be the group defined by following Cayley table , 1 2 3 4 5 6 17 1 2 3 4 5 6 7 2 2 3 4 1 6 7 5 3 4 2 7 4 2 5 4 6 6 4 7 6 2 1 4 7 6 5 4 2 (a) For each element a E G, Find the order of lal. (b) What is the center of G? (c) Find the centralizer of each member of G