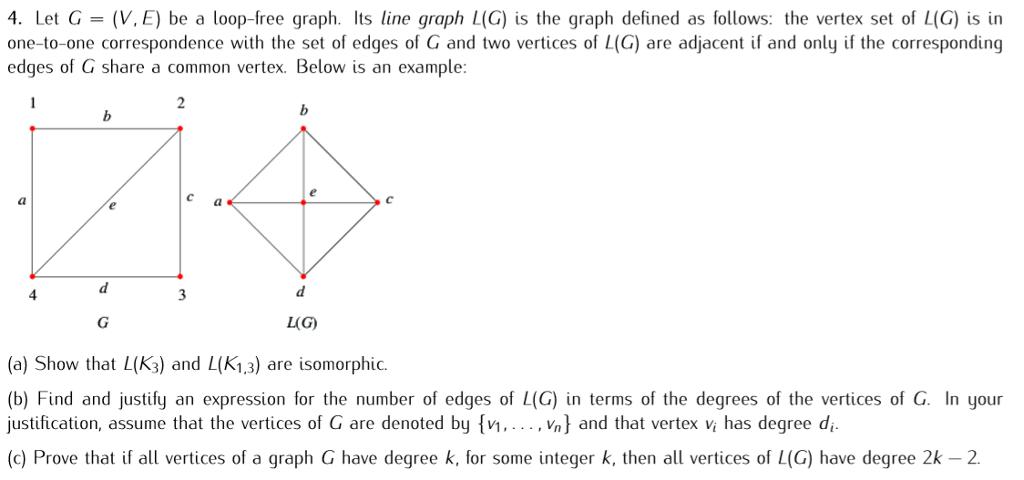
4. Let G = (V,E) be a loop-free graph. Its line graph L(G) is the graph defined as follows: the vertex set of L(G) is in one-to-one correspondence with the set of edges of G and two vertices of L(G) are adjacent if and only if the corresponding edges of G share a common vertex. Below is an example: 1 b 2 b a a d 4 3 d L(G) C G (a) Show that L(K3) and L(K1,3) are isomorphic. (b) Find and justify an expression for the number of edges of L(G) in terms of the degrees of the vertices of G. In your justification, assume that the vertices of G are denoted by {1,..., V} and that vertex v; has degree di. (c) Prove that if all vertices of a graph G have degree k, for some integer k, then all vertices of L(G) have degree 2k - 2.