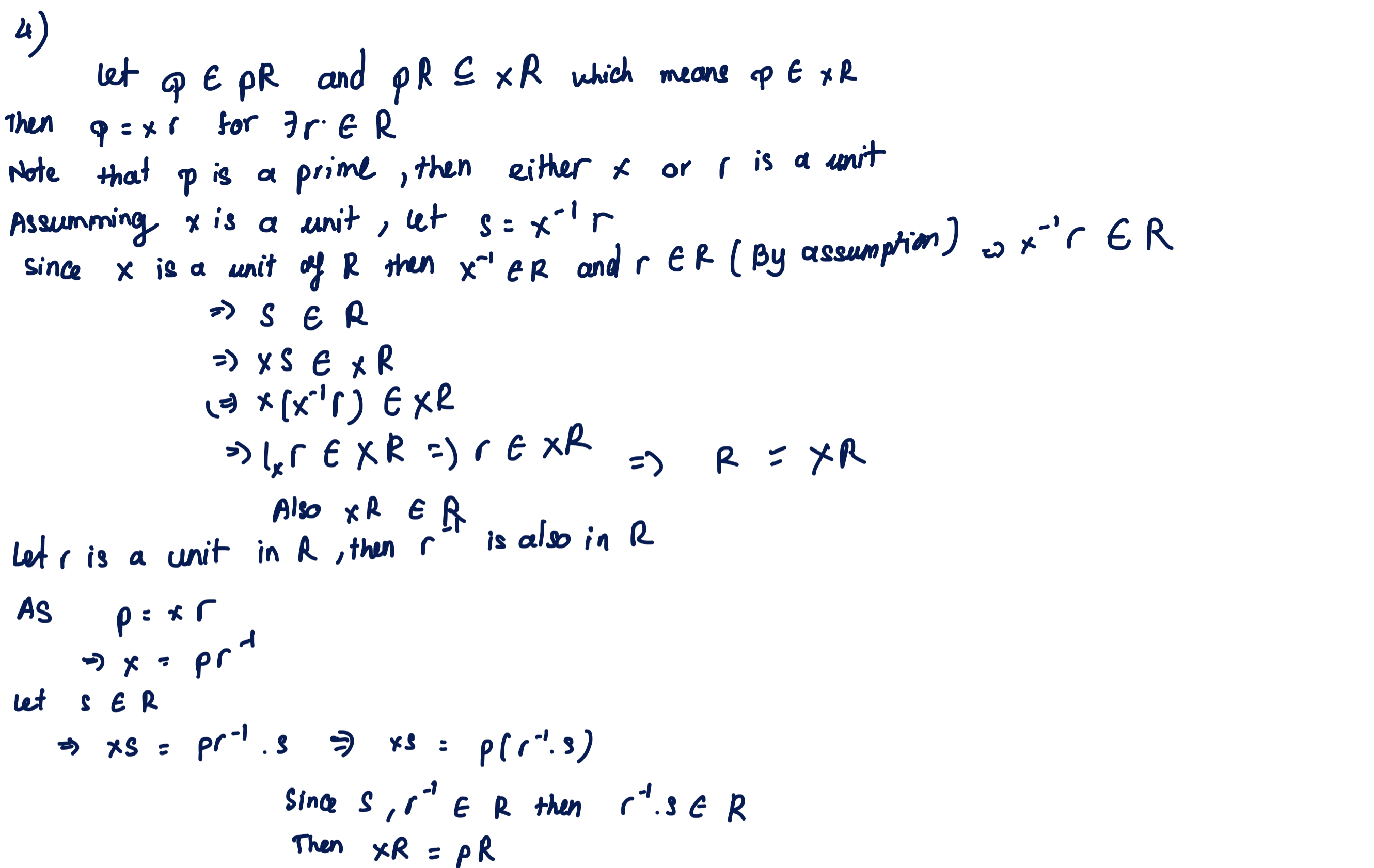
4) let P E PR and PR C XR which means op E x R Then QExr for Fri ER Note that p is a prime , then either f or , is a unit Assumming x is a unit , let s = *"'r Since X is a unit of R then x"ER and r ER ( By assumption) , x"'r ER - S ER = ) XS E x R 1 9) x ( x "'s ) EXR "> lrEXR = )(EX R =) RE XR Also XR ER Let's is a unit in R , then I"is also in R As p : x r let s ER xs = pr" . 3 5 xs = p(r 's) Since S , S" E R then r .3 G R Then XR = PR5 ) Assume that a, B is not a relative prime in 2 [Valj . There is a common divisor o for a, B where Sis not a unit of 2 I ra's Then = x, f and B= x, d (where x, # x2 and X,It, e Z[ ]) we have : Nodc (a) = No (x , J . N (8 ) No ( BJ = Nd ( X2 ) . Nd (8 ) from there : Nd 18) | Nd ( d ) and Nd (8 ) ( NoCP) Also : ged ( Nod (21 , Nd ( B ) ) = 1 By collary (i) in bezout's lemma = Nd (8) 1 1 = No ( 8 ) = 1 It shows 8 is a unit of ZIvaj - a contradicts Then a and B is a relative prime in 2 [ VOJ4. Let R be a ring and let x,p R with p prime. Assuming that pR C zR, prove that pR=xRor zR = R. We say that elements x and y in a ring R are relatively prime in R if their set of common divisors in R is precisely R* (the units). 5. Let d Z and assume v/d Q. Prove that, if a, 8 Z[v/d] have the property that ged(Ng(), Ng(B)) = 1, then o and 3 are relatively prime in Z[v/d]. (Hint: Let be a common divisor of a and in Z[/d]; the goal is to show that is a unit. One way to do this is to apply our favorite criterion for a quadratic integer to be a unit. Another is to use (a corollary of) Bzout's lemma.)