Question: 4. Let V C R be a subspace. Define VI = {u e R : u is orthogonal to V). In other words V! =

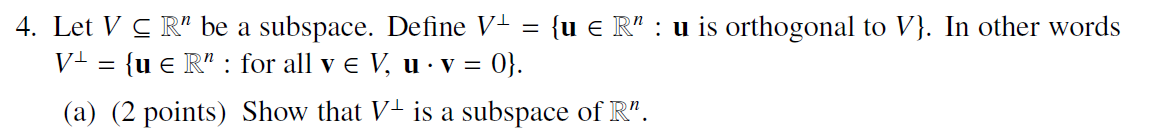
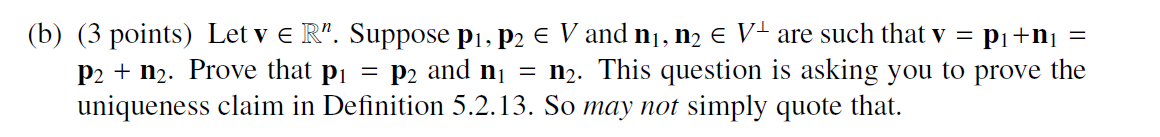
4. Let V C R" be a subspace. Define VI = {u e R" : u is orthogonal to V). In other words V! = {u e R" : for all v E V, u . v = 0). (a) (2 points) Show that V- is a subspace of R".(b) (3 points) Let v E R". Suppose p1, p2 E V and n1, n2 E V- are such that v = pitn = P2 + 12. Prove that p1 = p2 and n1 = n2. This question is asking you to prove the uniqueness claim in Definition 5.2.13. So may not simply quote that.(c) (3 points) Prove that (V-) = V.O O (d) (2 points) Let A = 0 Let C(A) denote the column space of A. Find a basis NO for C(A)+

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Choose the example that matches the value the example explains. Group of answer choices I can have a tattoo on my face if I choose. [ Choose ] Materialism Time and its control Individuality...

Let V C R" be a subspace. Define VI = (u e R" : u is orthogonal to V). In other words, V = (u ER" : u . v = 0 for all v E V). (a) (2 points) Show that Vis a subspace of R". (Hint: use Remark...

need help and please provide full solutions and explanations! Thank you!! Question 2. a) A unit vector U = in R2 is a vector of length | |3)| = va2 + 62 = 1. The goal of this exercise is to create a...

#5 Please The following preamble applies to both problems 4 and 5: Let W C R" be a subspace and let WA C R" be its orthogonal complement. Let S = fun,...; ux} be an orthogonal basis for W and S' =...

Please solve using this GS Method: Question 11 (10 marks) Consider R with the standard inner product given by the dot product (u, v) = u . v = ujuj + uzu2 + ugv3. Let W C R be the subspace spanned by...

Problem 4. We admit the following theorems. Theorem 3 (Standard matrix of a linear transformation). Let T : R" - R" be a linear transformation. Then T is a matrix transformation, i.e., T = TA, where...

(1) 4 Pts] a) Let V = Ro and consider the subspace Vo C V given by Vo = span {(1, -1, 1)}. Find the orthogonal complement Vo of Vo in V and find and an or- thonormal basis of the space Vo. b) Let V =...

Need correct solution of this problem, asap Question 4 Let V denote the real vector space of polynomials of degree at most 4. Define an inner product on V as follows: For polynomials f (x). g(x) EV,...

For Problems 1-3, let Mn (R) be the set of n x n matrices with real entries and define the subspace V = {AE M2(R) | A = A}. Define three ordered bases of V. Problem 1. (i) Find the 2 x 2 matrix A in...

: 3. (a) For a fixed b = R, let S = { = C[0,1] f f(x)dx = b}. Show that S is a subspace of C[0, 1] if and only if b = 0. (b) Let C-4,4] be the space of all continuous real-valued functions on [-4,4]....

7. Let P C R" be a nonempty polyhedron. The lineality space of P is the set lin( P) := recc(P) n (- recc(P)) = {d ER" : x + td E P Vx E P, VER} (a) Show that lin(P) is a linear subspace. (b) Show...

At a merging on-ramp of a busy Los Angeles freeway, car A is moving directly east on the freeway at a steady speed of 35.0 m/s. Car B is merging onto the freeway from the on-ramp, which points north...

Discuss the relative complexity of the two production systems.

Who is a Money Belt? Group of answer choices Sponsor / Champion who authorizes funding for the project Senior management who fund the project Finance department head Independent financial...

A company is preparing completing their Cash Budget. The following data has been prepared for cash receipts and payments. January February March Cash receipts $1,061,200 $1,182,400 $1,091,700 Cash...