Question: 4. Non-inertial frames (a) Using the chain rule, rewrite the D=2+1 Minkowski line element d-df+d + dy in polar coordinates: z=rcos, y=rsin 0, 1

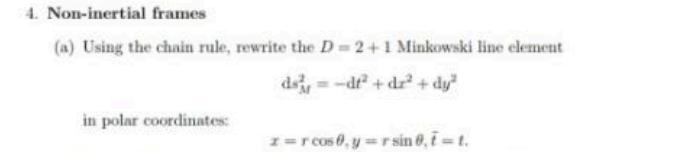
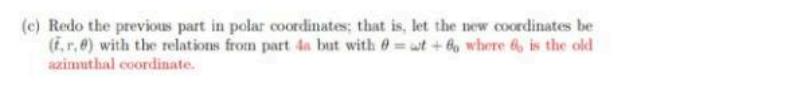
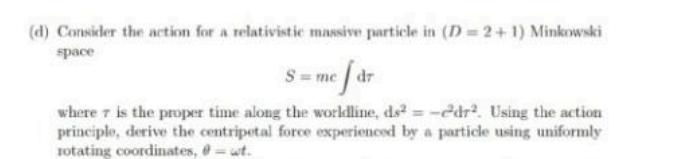
4. Non-inertial frames (a) Using the chain rule, rewrite the D=2+1 Minkowski line element d-df+d + dy in polar coordinates: z=rcos, y=rsin 0, 1 = t. (b) Rewrite ds in a rotating frame, where the new coordinates are cos ut sinut z= Rr, i=t. coswt) The new differentials are sinut (c) Redo the previous part in polar coordinates; that is, let the new coordinates be at +6o where 6, is the old (I. r.) with the relations from part 4a but with azimuthal coordinate. (d) Consider the action for a relativistic massive particle in (D=2+1) Minkowski space =me [dr where 7 is the proper time along the worldline, ds = -dr. Using the action principle, derive the centripetal force experienced by a particle using uniformly rotating coordinates, 0= wt.

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Using the chain rule for differentiation, show that the isobaric expansion coefficient expressed in terms of density is given by = (1/)(p/T) P .

Let z = ((x, y), where x = r cos ( and y = r sin (. Show that dr

A radius vector of a particle varies with time t as r = at (1 - at), where a is a constant vector and a is a positive factor. Find: (a) The velocity v and the acceleration w of the particle as...

Describe the overall organizational structure of the U.S. government's cybersecurity operations. What role does the Department of Homeland Security play in U.S. cybersecurity? Describe the division...

Please answer questions 3, 4, 5, and 6. Using the chain rule , find the derivative and simplify. (In the steps, nothing should be square rooted). Ignore the red pen mark.

How would I work these ? Can you give explanation please 1. Candace tried to find the derivative of the function y = h(x)e-4() but her group members disagreed with her result. What did she get right?...

Please do all the even numbers like 34, 36, 38, 40,42, 44, 46, 48, 50, 52, 54, 56, 58, 60, 62. . Please do it on paper bc it's really hard to understand when is written on here. Also, please show...

Use the chain rule to evaluate the derivative. 1. Find f'(x) if f(x) = (2x - 7)6. 2. Find [(4x3 - 7x) 4 ]. 3. Find [ ( 4X - 7) 4 (7 x + 8 ) 5 ] dx 4. Find d (4x - 7)3 dx (7x +8)3 Evaluate the first,...

This is all the information you need. Please follow all the steps. Read my sample posts carefully (below). ?In each sample post, I share evidence (an example) that the chain rule is important....

Let y = (2x + 3 sin(x))4. Find f (x) and g(x) so that y = f(g(x)) and compute the derivative using the Chain Rule. (Use symbolic notation and fractions where needed.) M = Calculate g 2 if f(u) = 5:8,...

Espresso Express operates a number of espresso coffee stands in busy suburban malls. The fixed weekly expense of a coffee stand is $1, 200 and the variable cost per cup of coffee served is $0.22....

Given the contents of the receipt.txt file; write a series of piped commands that will read the file and output a count of the number of lines that contain a negative number. receipt.txt Burrito...

The Secretary of the Interior recently announced the creation of the "Bring Waldo Home" project. When asked if this project was justified he responded that it would create over 8,000 jobs. Explain...

A new member of an agile development team believes it is unfair to track defect counts at the team level when the continuous integration tool identifies the developer associated with each logged...

King Builders gets a CIP for a $200 million construction program involving work in 12 states. Construction is expected to last two years. Which of the following suggests that the construction program...

When controlling priorities in production scheduling, economies of scope depend on decreasing which of the following costs or times? Group of answer choices Average cost per unit made Average cost to...

Cross Allantic Publishing was tecently organiced as a corporation. The company isscied common siock to an atlomey who provided legal servioes worth $15, ooo to help with the incorperaten Cross...

In your readings, there were many examples given for nurturing close family relationships in this ever-evolving technological society we live in Based upon your readings and research describe three...

Use Stokes Theorem to evaluate C F dr. In each case C is oriented counterclockwise as viewed from above, unless otherwise stated. F(x, y, z) = x 2 y i + x 3 j + e z tan 1 z k, C is the curve with...

Find the velocity, acceleration, and speed of a particle with the given position function. r(t) = (t 2 + t, t 2 t, t 3 )

Evaluate the integral. cos'x - dx csc x

The float associated with each project task can only be derived following the completion of the forward and backward passes. Explain why this is true.

Use the following information to determine the probability of this project finishing within 34 weeks of its scheduled completion date. Assume activities A B D F G are the projects critical path....

Consider the following information that you have compiled regarding the steps needed to complete a project. You have identified all relevant steps and have made some determinations regarding...