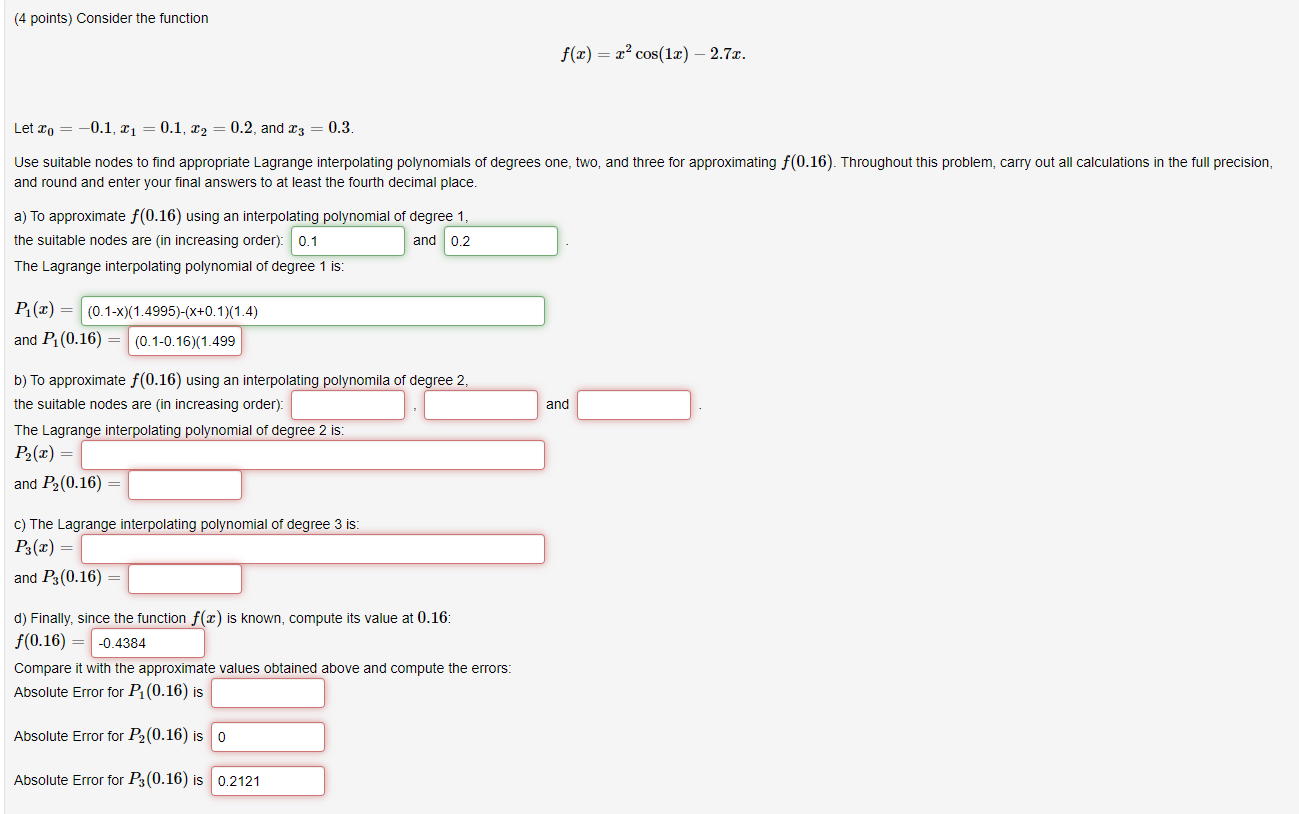
(4 points) Consider the function f()= x cos(12) - 2.72. Let to = -0.1, 21 0.1, 12 0.2, and 23 = 0.3 Use suitable nodes to find appropriate Lagrange interpolating polynomials of degrees one, two, and three for approximating f(0.16). Throughout this problem, carry out all calculations in the full precision, and round and enter your final answers to at least the fourth decimal place. a) To approximate f(0.16) using an interpolating polynomial of degree 1, the suitable nodes are in increasing order): 0.1 and 0.2 The Lagrange interpolating polynomial of degree 1 is: P1(x) = (0.1-x)(1.4995)-(x+0.1)(1.4) and P10.16) = (0.1-0.16)(1.499 and b) To approximate f(0.16) using an interpolating polynomila of degree 2, the suitable nodes are in increasing order) The Lagrange interpolating polynomial of degree 2 is: P2(30) = and P2 (0.16) c) The Lagrange interpolating polynomial of degree 3 is: P3(2) = and P3 (0.16) d) Finally, since the function f(2) is known, compute its value at 0.16: f(0.16) = -0.4384 Compare it with the approximate values obtained above and compute the errors: Absolute Error for P(0.16) is Absolute Error for P2(0.16) is O Absolute Error for P3(0.16) is 0.2121