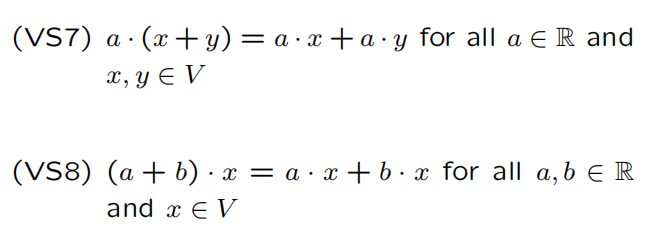
(4 points) Suppose that (V, +, .) is a vector space and x, y E V. Show directly from (VS1)- 1 (VS8) that if y + - . x = x then x = 2 . y. Specify which of (VS1)-(VS8) are used in your proof.\fA vector space over R is a tuple (V, +, .) where V is a set, + : V x V -> V and . : Rx V - V such that (VS1) xty = y + x for all x, y EV (VS2) (x ty) +z = x+(y+z) for all x, y, z EV (VS3) there exists 0 E V such that x + 0 = x for all x E V (VS4) for every x E V, there exists -x E V such that a + (-x) = 0 (VS5) 1 . x = x for all x EV (VS6) (ab) . x = a . (b . x) for all a, b E R and DEV