Question: 4. Solve the initial-value problem dy 14x + 10 y(1) = 0 dx T5. Find an equation of the curve that satisfies the given conditions:
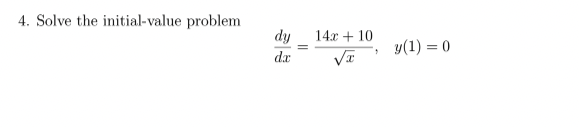
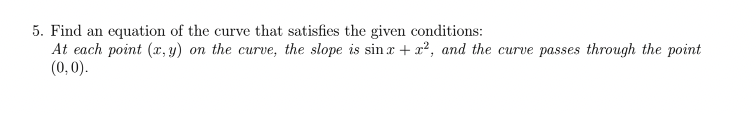



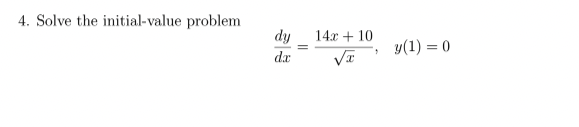
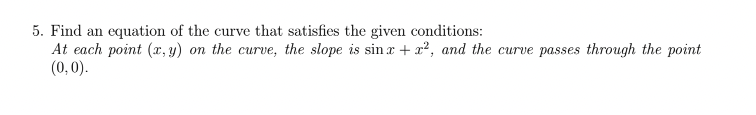
![10] and differentiable function in (1, 10). Assume that f(1) = 12](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6665565c102b2_2766665565c00897.jpg)


4. Solve the initial-value problem dy 14x + 10 y(1) = 0 dx T5. Find an equation of the curve that satisfies the given conditions: At each point (x,y) on the curve, the slope is sina + c', and the curve passes through the point (0, 0).6. Find the position function s(t) of a particle given that its acceleration a(t) = 1 + 4, and its initial values v(0) = 5, and s(0) = 5.8. Let f(x) be a continuous function on [1, 10] and differentiable function in (1, 10). Assume that f(1) = 12 and f'(x) 0 for all x and f"(x) 0. Is the approximation found in part (b) an overestimate or underestimate for f(1.8)? Justify. (d) Using the Mean Value Theorem, explain why the average rate of change of f over the interval 1
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


