Question: 4. Use Step 3 to show that a function that is continuous on [a, b] and is symmetric about the point ((a + b)/2, f((a
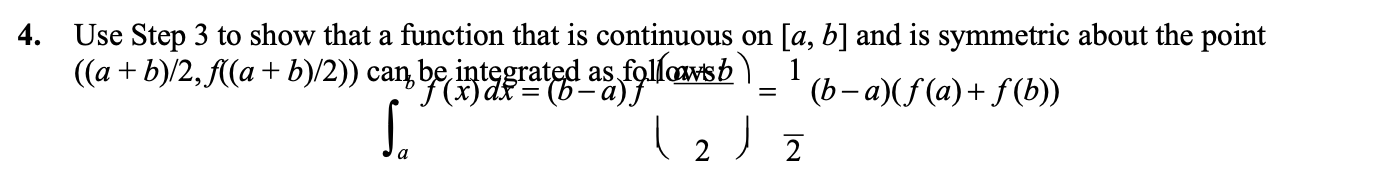
![continuous on [a, b] and is symmetric about the point ((a +](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6665ef610ff0f_4486665ef60e4e2e.jpg)
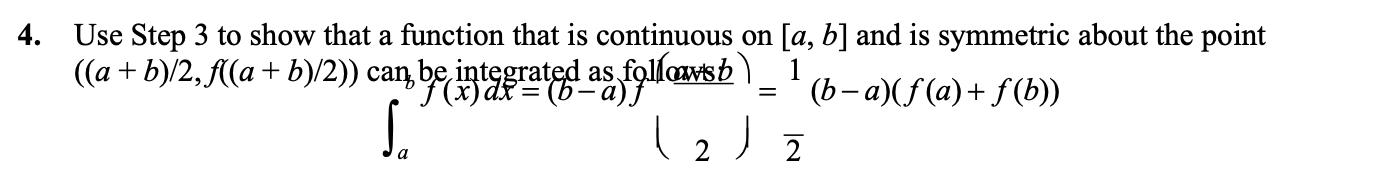
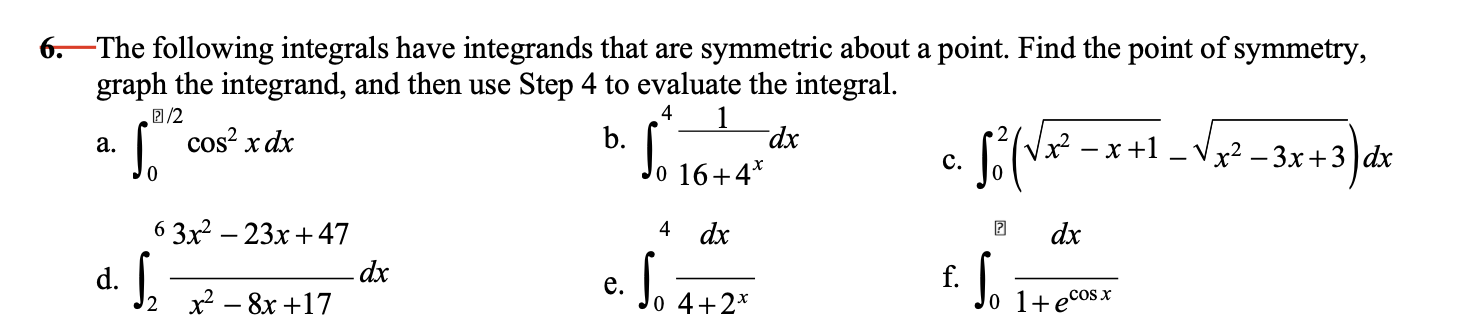
4. Use Step 3 to show that a function that is continuous on [a, b] and is symmetric about the point ((a + b)/2, f((a + b)/2)) can, be integrated as followsb ) 1 (x) di = (b - a) f = (b - a)(f (a) + f(b)) a 2 26. The following integrals have integrands that are symmetric about a point. Find the point of symmetry, graph the integrand, and then use Step 4 to evaluate the integral. 2 /2 4 a. cos x dx b. dx Jo 16+4x c. So( VX - x +1 x2 - 3x + 3 dx 6 3x2 - 23x + 47 4 dx dx d. dx J2 x2 - 8x +17 e. Jo 4+2x f. 0 1+ ecosx
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


