Question: 4. Write a computer program that evaluates Pn(x) where Pn(x) is the Taylor series expansion derived in problem (3) above. Verify that If(x) Pn(x)l satisfies

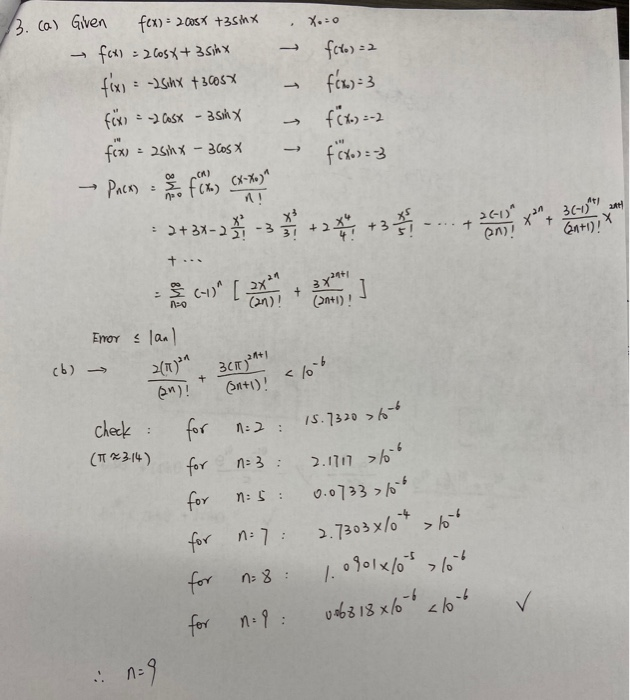
4. Write a computer program that evaluates Pn(x) where Pn(x) is the Taylor series expansion derived in problem (3) above. Verify that If(x) - Pn(x)l satisfies the appropriate error bound. You must be able to convince me by plotting results and checking the error for your approximation that everything was programmed correctly. From your graphs, you will see that the error depends on. Which values of x would you predict tend to give smaller/larger errors? Does your graph corroborate your intuition? 3. Let f(x) = 2 cos(x) + 3 sin(x) and Xo = 0. Find the nth Taylor polynomial Pn(x) for f(x) about 30. Find a value n necessary for Pn () to approxi- mate f(x) to within 10-6 on (-7,7). For which values of x is the series guaranteed to converge? 1 X.o foto) = 2 f(x) = 3 1 3.ca) Given fex) = 2005* +35iX - fox) = 2605*+ 35hx f(x) = -2 Schx + 300sx fm --> 00SX - 35 x fx = 25inx - 3cosx - Pacos CCM k. " 1 f(x) = -2 fx=3 + .. (1)" [ Error & lan) 2/10) n (6) t 3C124+ (anti)i check (TT *3-14) for for for anti)! N:2: 15.7320 > toto n=3 : 2.1717 lo" nis: 0.0733>/03 n=7: 2.73030/0 * > lot n=8: 1.0801x/os/66 n. 9: 86818x60
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


