4.1A: Draw the decision tree for Mergesort (Algorithm 4.5, Page 175), which uses Merge (Algorithm 4.4, Page 172) when n=3. To get this right, you'll have to carefully examine the code at the bottom of page 175; remember that array numbering starts at index zero, and that integer division *truncates* (it doesn't round).

#172

#175

This is the similar diagram on page 178, but the one needed to be drawn is slightly different:

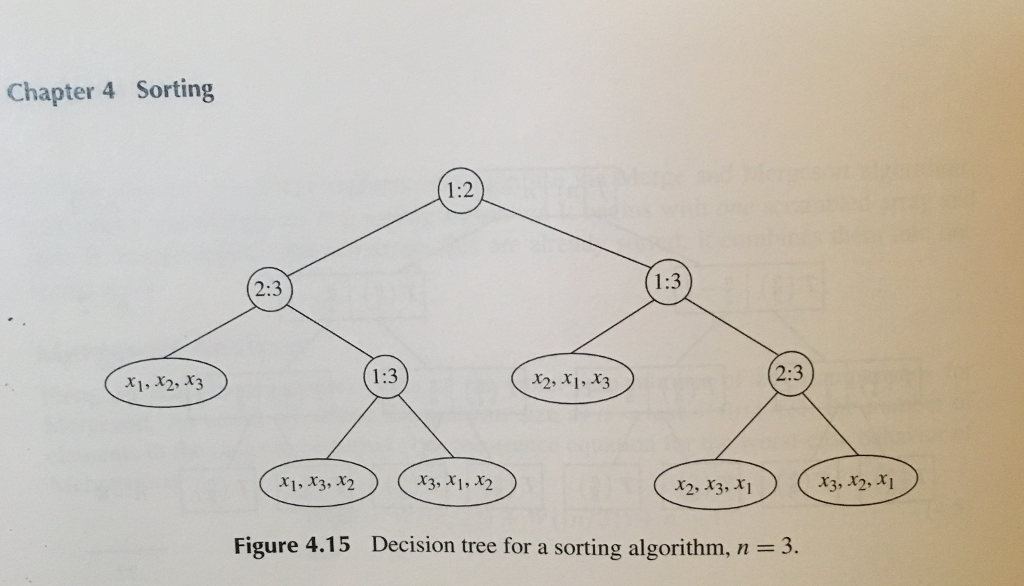
4.1B: Based on *your* decision tree in 4.1A, determine the average number of comparisons done by Mergesort when n=3. (Do NOT try to plug into some formula; I am simply asking you to examine your decision tree and count the number of comparisons, taking a weighted average to find the exact answer.)

L(first + last)/2] first last Sort recursively by Mergesort Sort recursively by Mergesort Sorted Sorted Merge Sorted Figure 4.13 Mergesort strategy Thus, using the divide-and-conquer terminology of Section 4.3, divide merely computes the middle index of the subrange and does no key comparisons; combine does the merging. We assume that Merge is modified to merge adjacent subranges of one array, putting the resulting merged array back into the cells originally occupied by the elements being merged. Its parameters now are the array name E, and the first, mid, and last indexes of the subranges it is to merge; that is, the sorted subranges are E[first),..., Elmid] and E[mid+1 1. Elast], and the final sorted range is to be E[first],..., Ellast]. In this modification, the merge subroutine is also responsible for allocating additional workspace needed. Some of the issues were discussed in Section 4.5.3