Question: 4.2. Use the numerical values in the table below to fit a spherical model on the above (table1) experimental semi-variogram. Distance between samples (m)

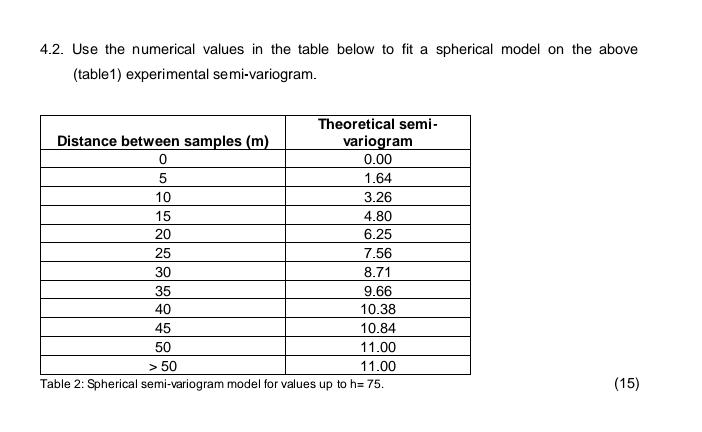
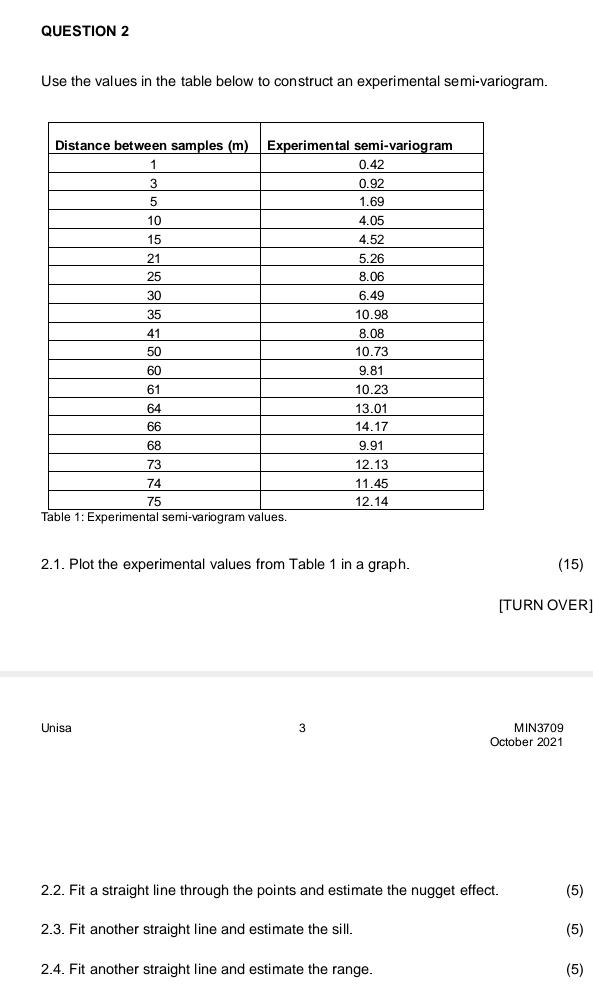
4.2. Use the numerical values in the table below to fit a spherical model on the above (table1) experimental QUESTION 2 Use the values in the table below to construct an experimental semi-variogram. Distance between

4.2. Use the numerical values in the table below to fit a spherical model on the above (table1) experimental semi-variogram. Distance between samples (m) 0 5 10 15 20 25 30 35 40 Theoretical semi- variogram 0.00 1.64 3.26 4.80 6.25 7.56 8.71 9.66 10.38 10.84 11.00 11.00 Table 2: Spherical semi-variogram model for values up to h= 75. 45 50 > 50 (15) QUESTION 2 Use the values in the table below to construct an experimental semi-variogram. Distance between samples (m) Experimental semi-variogram 1 3 5 10 15 21 25 30 35 41 50 60 61 64 66 68 73 74 75 Table 1: Experimental semi-variogram values. Unisa 0.42 0.92 1.69 4.05 4.52 3 5.26 8.06 2.1. Plot the experimental values from Table 1 in a graph. 6.49 10.98 8.08 10.73 9.81 10.23 13.01 14.17 9.91 12.13 11.45 12.14 (15) [TURN OVER] 2.4. Fit another straight line and estimate the range. MIN3709 October 2021 2.2. Fit a straight line through the points and estimate the nugget effect. 2.3. Fit another straight line and estimate the sill. (5) (5) (5)

Step by Step Solution

★★★★★

3.45 Rating (152 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

FOR 21 Plot the experimental values from the tabl... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Use the survey results in the table below to investigate differences in employee job satisfaction among organizations in the United States with different management styles. a) Select the appropriate...

Use the data values in the table below to calculate the correlation between the variables x and y. x y 4 30.72 5 30.06 6 26.4 7 23.64 8 19.88 9 19.52 10 14.56 11 13.7 Give your answer to three...

Use the data in the table below to answer questions (a) through (d). (a) What was the rate of growth of real GDP from 2016 to 2017, and 2017 to 2018? (b) What was the rate of inflation in 2017 and in...

Allen maintains a two-column cash book. The following transactions have taken place using the business bank account: Required Enter the transactions in the cash book. 1 July 4 July 6 July 7 July 8...

In Problems 7-18, a sample of paired data gives a linear correlation coefficient $r$. In each case, use Table 14.10 to determine whether there is a significant linear correlation. Table 14. 10...

A company selling an air conditioner has estimated the market capacity as 50000 units a year. The directors have set the company a sales objective of between 50 per cent and 80 per cent of this...

A freshly brewed shot of espresso has three distinct components: the heart, body, and crema. The separation of these three components typically lasts only 10 to 20 seconds. To use the espresso shot...

Refer to the Nuclear Energy Institute's list of all states with active nuclear power plants, Exercise 2.54. The data on number of power plants per state are reproduced in the accompanying table. Note...

The following table gives data on median salaries of full professors in statistics in research universities in the United States for the academic year 2007. a. Plot median salaries against years in...

10. Suppose you invest $30,000 in a CD on January 1, 2020 maturing in 14 years that pays interest of 6% per year compounded quarterly (meaning every three months) and credited at the end of each...

Describe credit scoring and explain how its used (by lenders) in making a credit decision.

code class = "asciimath" > ( 0 , 5 ) Sobre o baricentro, julgue as afirmativas a seguir: 1 - - O baricentro sempre um ponto interno do triangulo. | | - > O baricantro o ponto de encontro das...

The statement of cash flows for a government hospital would differ from that of a private not for-profit hospital. The following represent a hospital's inflows and outflows of cash: Patient service...

The Office of the Treasurer operates an investment pool. Owing to risky investments and an increase in interest rates, the market value of pool securities has substantially declined. By publicizing...

There are many types of information that require assurance. Individually or in groups, identify the following types of assurance services. a. Identify three or more assurance services that are likely...

Starling Company purchased machinery at the beginning of Year 1 at a cost of $86,100. The machinery has an estimated life of five years and an estimated residual value of $4,305. Accumulated...

What types of problems might the culturally diverse top-management team at headquarters create for the joint venture? Give some specific examples. How could these problems be overcome?

Right answer Question 1 of 12 A prompt is anything that will hint or cue the person to perform the desired behavior. True False

Jupyter Notebook Now that we have tried our hand at some single-layer nets, let's see how they stack up compared to multi-layer nets. :) We will be exploring the basic concepts of learning non-linear...

I have an assignment where you need an experiment design study from Golub study. (NEED TO USE R PROGRAMMING). The script of the R program for the assignment is below. The assignment is attached...

Find attached Ingredients: Water, MCC, Salt, Nicotine, pH regulator, sweeteners and flavours I am wondering why the decision to go with LYFT. I understand migrating to LYFT would be easier from sells...

An Investigation into obesity rates Researchers have been interested in studying the obesity trends worldwide over the past 25 years. In 2014 the World Health Organization (WHO) declared there were....

Ring method (manual method) The main instrument is an electronic balance by Lauda. It can be used for surface tension measurements following du Noy (ring), Wilhelmy (plate), or Lenard (wire), as well...

It appears that because of COVID limitations, data was collected virtually through phone, email, and surveys with a population that may have barriers to those methods of data collection. How do you...