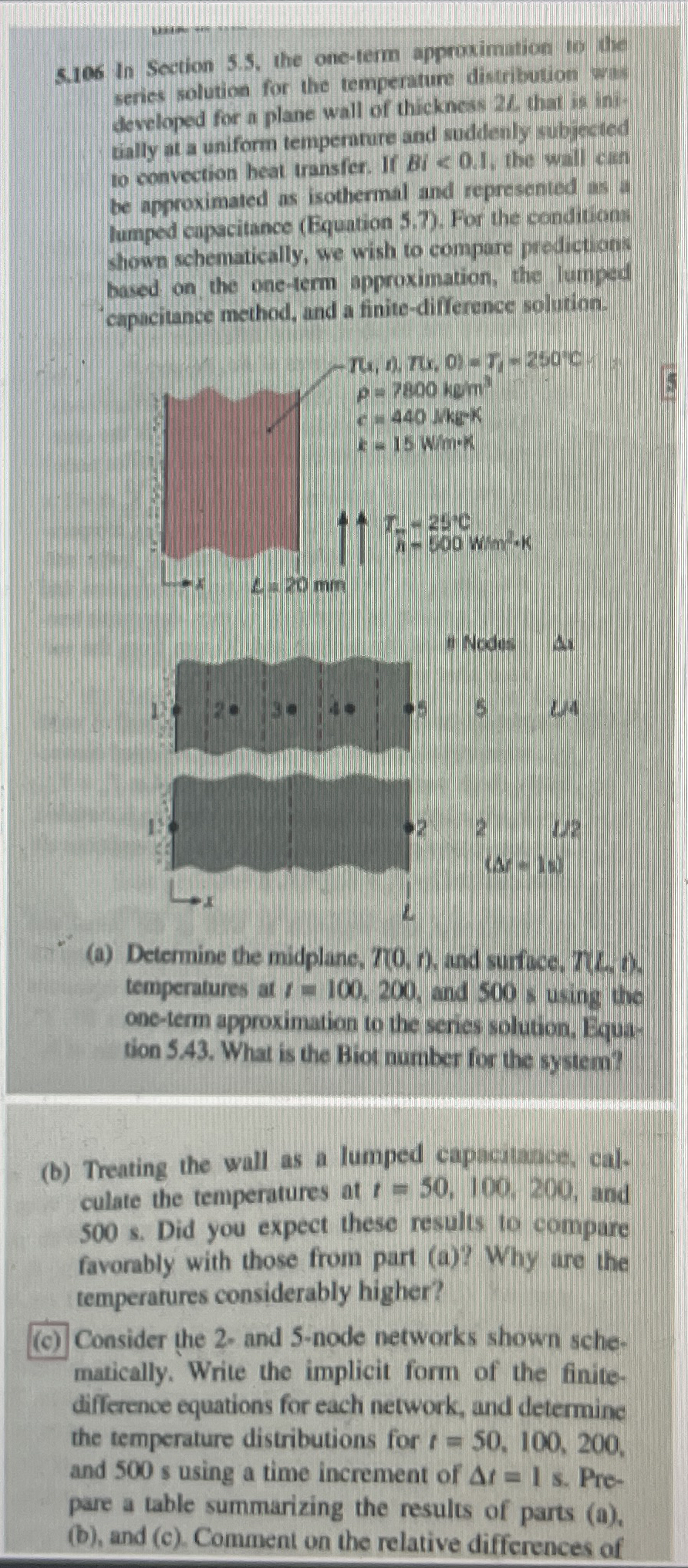
Question: 5 . 1 0 6 In Section 5 . 5 , the one - term approximution th the series solution for the temperature discribution wat
In Section the oneterm approximution th the
series solution for the temperature discribution wat
developed for a plane wall of thickncss that in ini
tially at a uniform temperarure and suddenly subjected
to convection heat transfer. If the waill cin
lumped capacitance Equation For the condition
shown schematically, we wish to compare predictions
based on the oneterm approximation, the lutmped
Capacitance method, and a finitedifference solytion.
MkeK
Win
a Determine the midplane, and surfoce,
temperatures at and susing the
oneterm approximation to the senes solution, Equa
tion What is the Biot number for the system?
b Treating the wall as a lumped capacalangen cal.
culate the temperatures at and
s Did you expect these results to compare
favorably with those from part a Why are the
temperarures considerably higher?
c Consider the and node networks shown sche
matically, Write the implicit form of the finite
difference equations for each network, and determine
the temperature distributions for
and s using a time increment of s Pre
pare a table summarizing the results of parts
b and c Comment on the relative differences of
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


