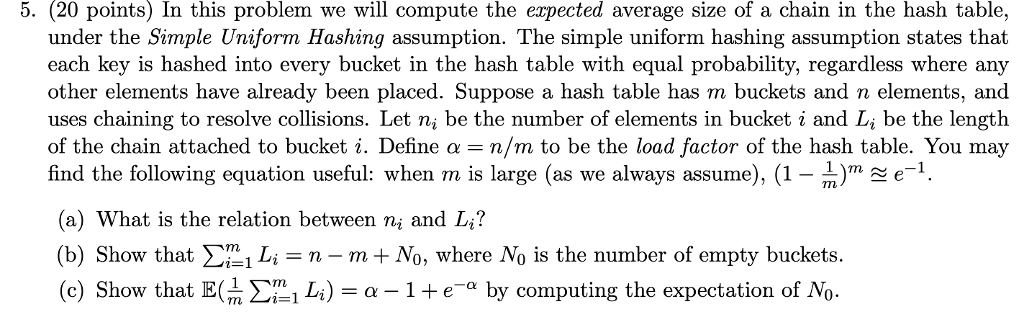
5. (20 points) In this problem we will compute the expected average size of a chain in the hash table, under the Simple Uniform Hashing assumption. The simple uniform hashing assumption states that each key is hashed into every bucket in the hash table with equal probability, regardless where any other elements have already been placed. Suppose a hash table has m buckets and n elements, and uses chaining to resolve collisions. Let n, be the number of elements in bucket i and L, be the length of the chain attached to bucket i. Define a -n/m to be the load factor of the hash table. You may find the following equation useful: when m is large (as we always assume), 1-)m. Let n, be the number of elements in bucket i and Li be the length (a) What is the relation between ni and L? (b) Show that i-1 Li-n-m + M0, where o is the number of empty buckets. (c) Show thatEa1ea by computing the expectation of No 5. (20 points) In this problem we will compute the expected average size of a chain in the hash table, under the Simple Uniform Hashing assumption. The simple uniform hashing assumption states that each key is hashed into every bucket in the hash table with equal probability, regardless where any other elements have already been placed. Suppose a hash table has m buckets and n elements, and uses chaining to resolve collisions. Let n, be the number of elements in bucket i and L, be the length of the chain attached to bucket i. Define a -n/m to be the load factor of the hash table. You may find the following equation useful: when m is large (as we always assume), 1-)m. Let n, be the number of elements in bucket i and Li be the length (a) What is the relation between ni and L? (b) Show that i-1 Li-n-m + M0, where o is the number of empty buckets. (c) Show thatEa1ea by computing the expectation of No