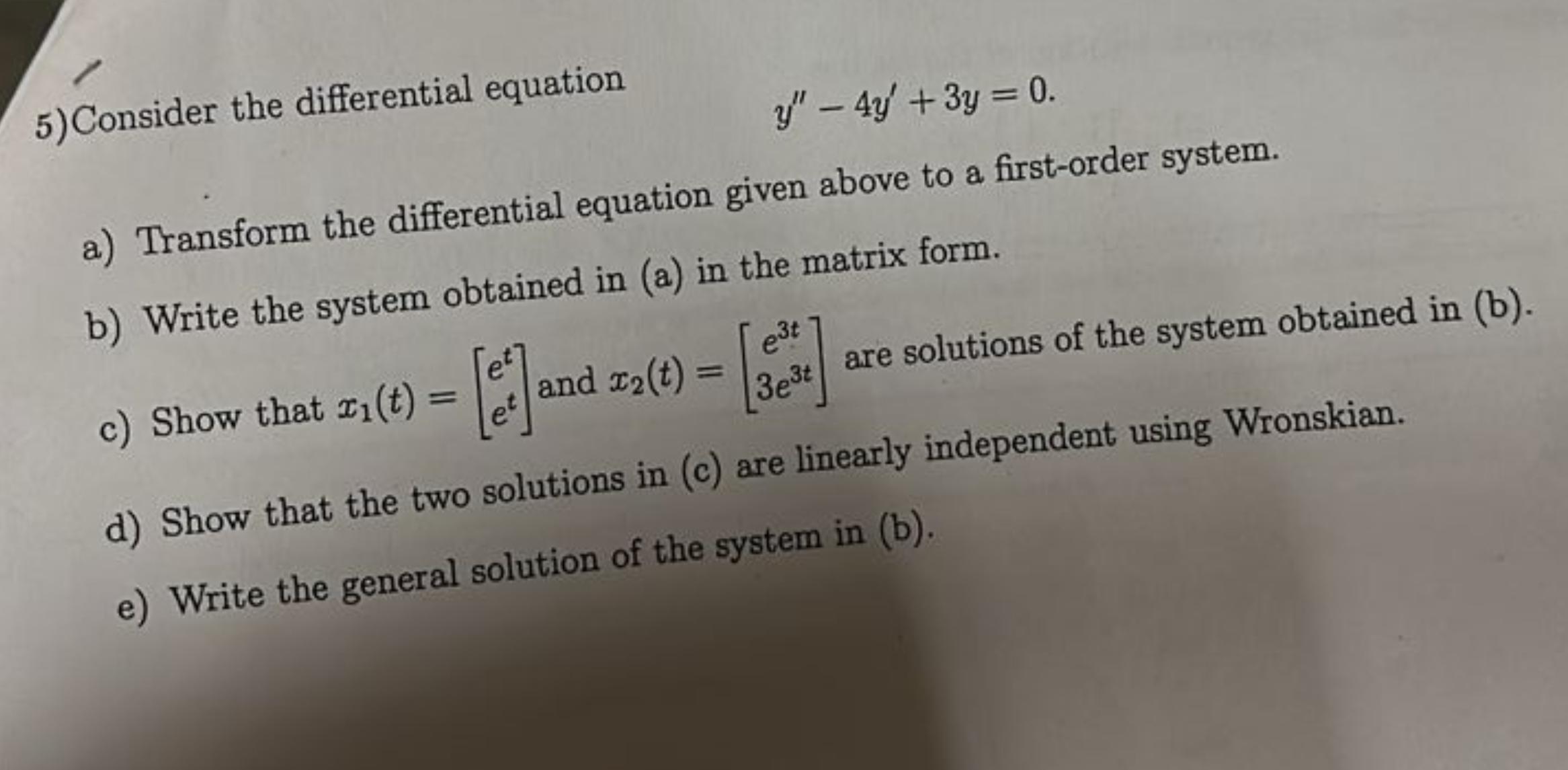
5) Consider the differential equation y" - 4y' + 3y = 0. a) Transform the differential equation given above to a first-order system. b) Write the system obtained in (a) in the matrix form. et et c) Show that x1(t) = [] and x2(t) = e3t are solutions of the system obtained in (b). 3e3t d) Show that the two solutions in (c) are linearly independent using Wronskian. e) Write the general solution of the system in (b).