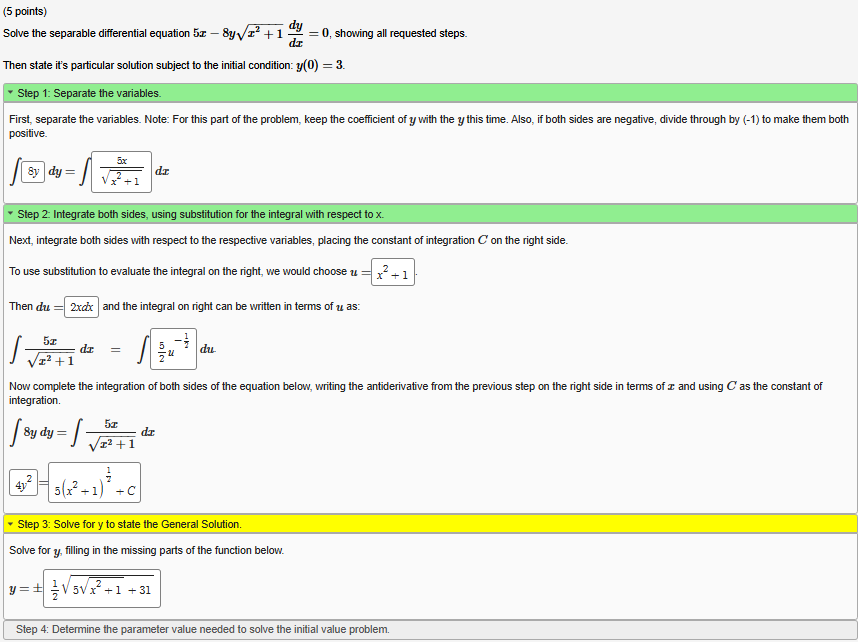
$(5$ points$)$

Solve the separable differential equation $5$x$-8$y$\backslash$sqrt$($x$^(2)+1)($dy$)/($dx$)=0,$ showing all requested steps.

Then state if's particular solution subject to the initial condition: y$(0)=3.$

Step $1$: Separate the variables.

First, separate the variables. Note: For this part of the problem, keep the coefficient of y with the y this time. Also, if both sides are negative, divide through by $(-1)$ to make them both

positive.

$\backslash$int dy$=\backslash$int $\backslash$sqrt$()$dx

Step $2$: Integrate both sides, using substitution for the integral with respect to x$.$

Next, integrate both sides with respect to the respective variables, placing the constant of integration C on the right side.

To use substitution to evaluate the integral on the right, we would choose u$=$

Then du$=|,$ and the integral on right can be written in terms of u as:

$\backslash$int $(5$x$)/(\backslash$sqrt$($x$^(2)+1))$dx$=\backslash$int $,$du

Now complete the integration of both sides of the equation below, writing the antiderivative from the previous step on the right side in terms of x and using C as the constant of

integration.

$\backslash$int $8$ydy$=\backslash$int $(5$x$)/(\backslash$sqrt$($x$^(2)+1))$dx

$4$y$^(2)=$

Step $3$: Solve for y to state the General Solution.

Solve for y$,$ filling in the missing parts of the function below.

y$=+-$uarr

Step $4$: Determine the parameter value needed to solve the initial value problem.