Solve only PART 2.

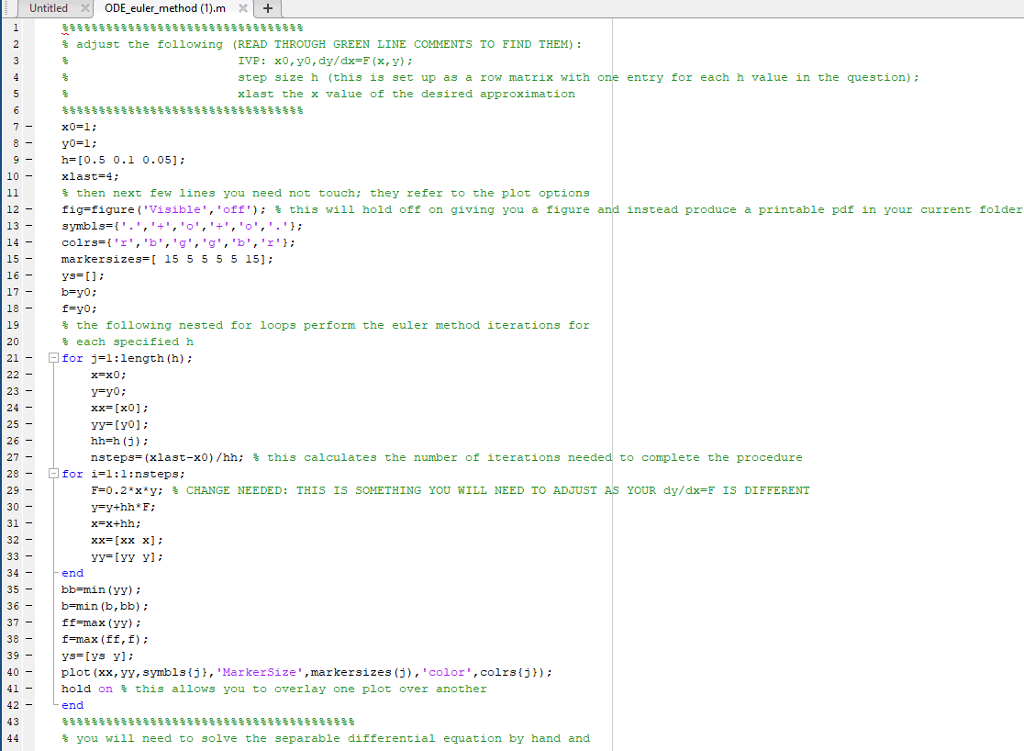
Please write down the changes of any line and provide the number of the line.

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

% adjust the following (READ THROUGH GREEN LINE COMMENTS TO FIND THEM):

% IVP: x0,y0,dy/dx=F(x,y);

% step size h (this is set up as a row matrix with one entry for each h value in the question);

% xlast the x value of the desired approximation

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

x0=1;

y0=1;

h=[0.5 0.1 0.05];

xlast=4;

% then next few lines you need not touch; they refer to the plot options

fig=figure('Visible','off'); % this will hold off on giving you a figure and instead produce a printable pdf in your current folder

symbls={'.','+','o','+','o','.'};

colrs={'r','b','g','g','b','r'};

markersizes=[ 15 5 5 5 5 15];

ys=[];

b=y0;

f=y0;

% the following nested for loops perform the euler method iterations for

% each specified h

for j=1:length(h);

x=x0;

y=y0;

xx=[x0];

yy=[y0];

hh=h(j);

nsteps=(xlast-x0)/hh; % this calculates the number of iterations needed to complete the procedure

for i=1:1:nsteps;

F=0.2*x*y; % CHANGE NEEDED: THIS IS SOMETHING YOU WILL NEED TO ADJUST AS YOUR dy/dx=F IS DIFFERENT

y=y+hh*F;

x=x+hh;

xx=[xx x];

yy=[yy y];

end

bb=min(yy);

b=min(b,bb);

ff=max(yy);

f=max(ff,f);

ys=[ys y];

plot(xx,yy,symbls{j},'MarkerSize',markersizes(j),'color',colrs{j});

hold on % this allows you to overlay one plot over another

end

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

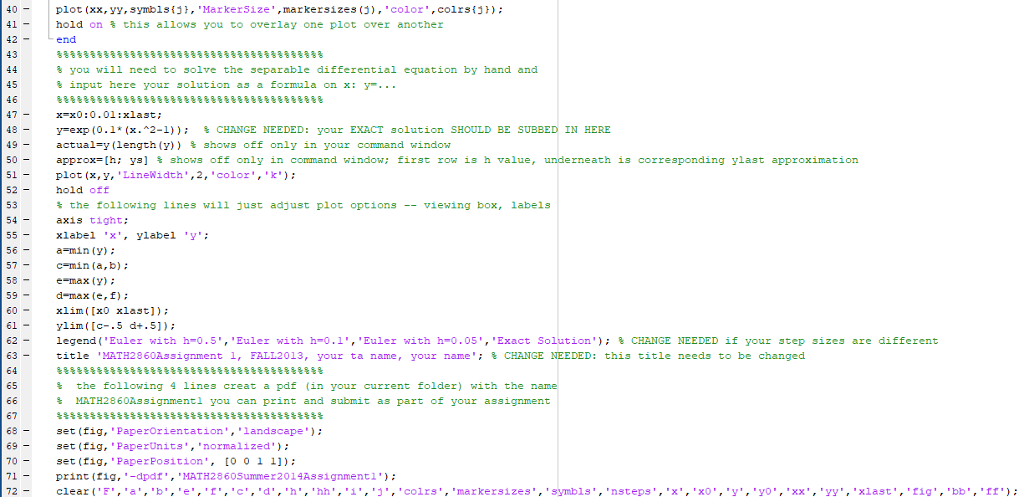
% you will need to solve the separable differential equation by hand and

% input here your solution as a formula on x: y=...

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

x=x0:0.01:xlast;

y=exp(0.1*(x.^2-1)); % CHANGE NEEDED: your EXACT solution SHOULD BE SUBBED IN HERE

actual=y(length(y)) % shows off only in your command window

approx=[h; ys] % shows off only in command window; first row is h value, underneath is corresponding ylast approximation

plot(x,y,'LineWidth',2,'color','k');

hold off

% the following lines will just adjust plot options -- viewing box, labels

axis tight;

xlabel 'x', ylabel 'y';

a=min(y);

c=min(a,b);

e=max(y);

d=max(e,f);

xlim([x0 xlast]);

ylim([c-.5 d+.5]);

legend('Euler with h=0.5','Euler with h=0.1','Euler with h=0.05','Exact Solution'); % CHANGE NEEDED if your step sizes are different

title 'MATH2860Assignment 1, FALL2013, your ta name, your name'; % CHANGE NEEDED: this title needs to be changed

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

% the following 4 lines creat a pdf (in your current folder) with the name

% MATH2860Assignment1 you can print and submit as part of your assignment

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

set(fig,'PaperOrientation','landscape');

set(fig,'PaperUnits','normalized');

set(fig,'PaperPosition', [0 0 1 1]);

print(fig,'-dpdf','MATH2860Summer2014Assignment1');

clear('F','a','b','e','f','c','d','h','hh','i','j','colrs','markersizes','symbls','nsteps','x','x0','y','y0','xx','yy','xlast','fig','bb','ff');

dy_ycos2 x sin x-0, y(?/2) 1 1. Solve the IVP above. (You must do this by hand and submit one neat 2. Use Euler's method to approximate the solution for r values between copy per group.) 0 and 3 using the matlab file provided (make the appropriate changes in that file) with step sizes h 0.1, h = 0.05, h = 0.01. NOTE: running the matlab file will produce a pdf file that each member of the group should print and attach to the as- signme nt submission