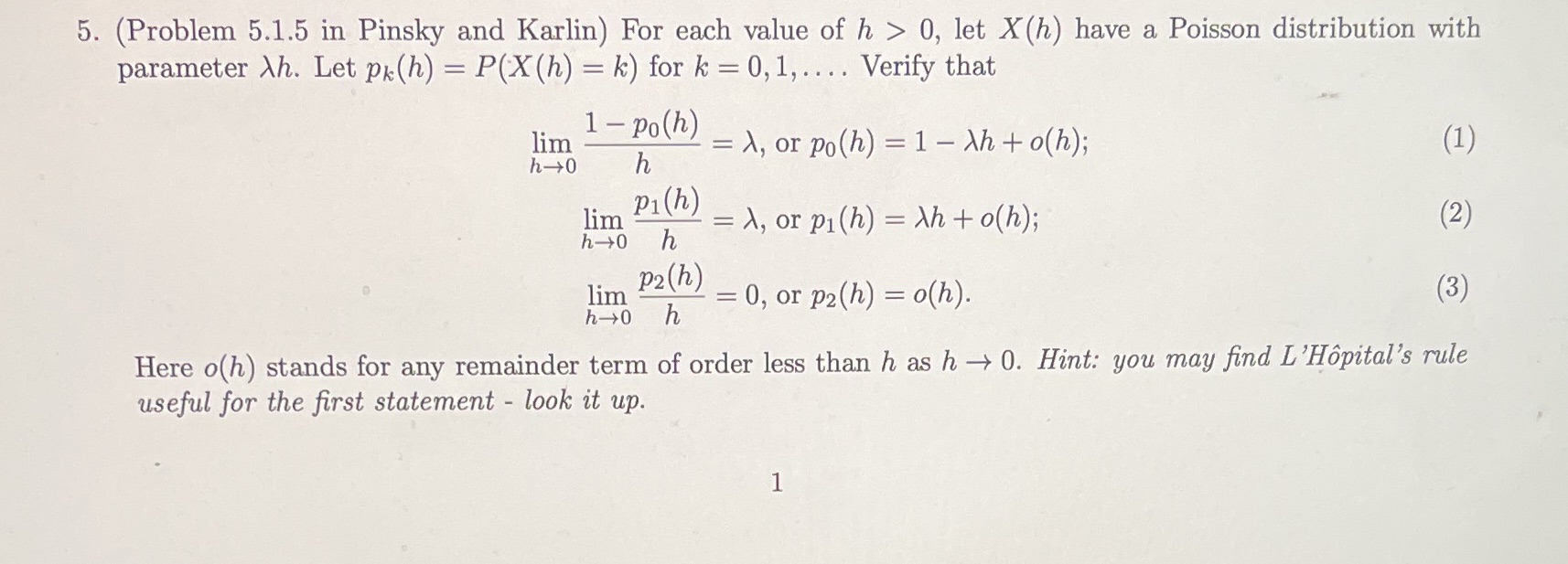
5. (Problem 5.1.5 in Pinsky and Karlin) For each value of h > 0, let X(h) have a Poisson distribution with parameter Ah. Let Pk(h) = P(X(h) = k) for k = 0, 1, .... Verify that lim 1 - Po(h) = 1, or po(h) = 1 - Ah + o(h); h -+0 h (1) lim P1 (h) = 1, or pi(h) = Ah + o(h); (2) ho h lim p2(h) h = 0, or p2(h) = o(h). 3 h-+0 Here o( h) stands for any remainder term of order less than h as h - 0. Hint: you may find L'Hopital's rule useful for the first statement - look it up