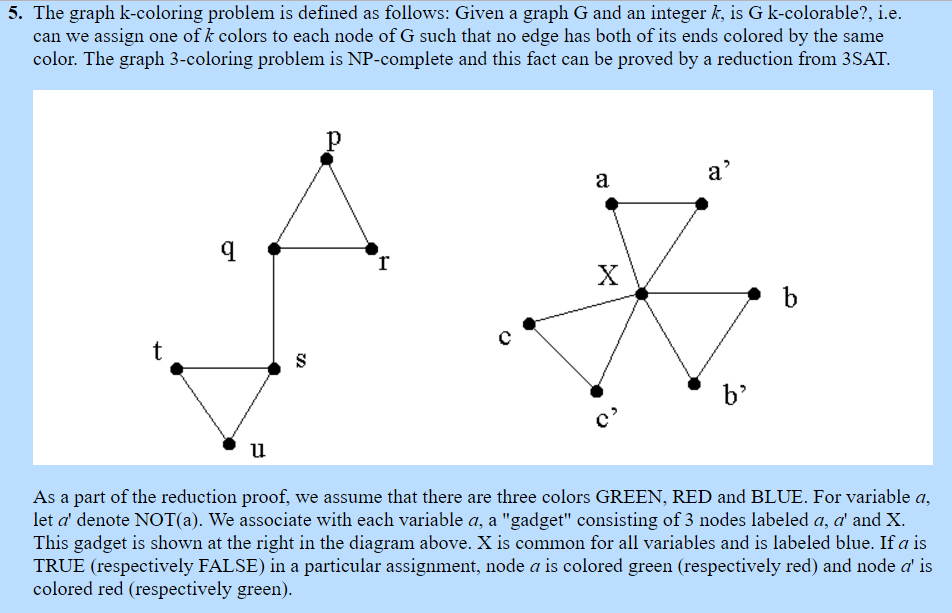
5. The graph k-coloring problem is defined as follows: Given a graph G and an integer k, is G k-colorable?, i.e. can we assign one of k colors to each node of G such that no edge has both of its ends colored by the same color. The graph 3-coloring problem is NP-complete and this fact can be proved by a reduction from 3SAT. b' As a part of the reduction proof, we assume that there are three colors GREEN, RED and BLUE. For variable a, let a' denote NOT(a). We associate with each variable a, a "gadget" consisting of 3 nodes labeled a, a' and X This gadget is shown at the right in the diagram above. X is common for all variables and is labeled blue. If a is TRUE (respectively FALSE) in a particular assignment, node a is colored green (respectively red) and node a' is colored red (respectively green)