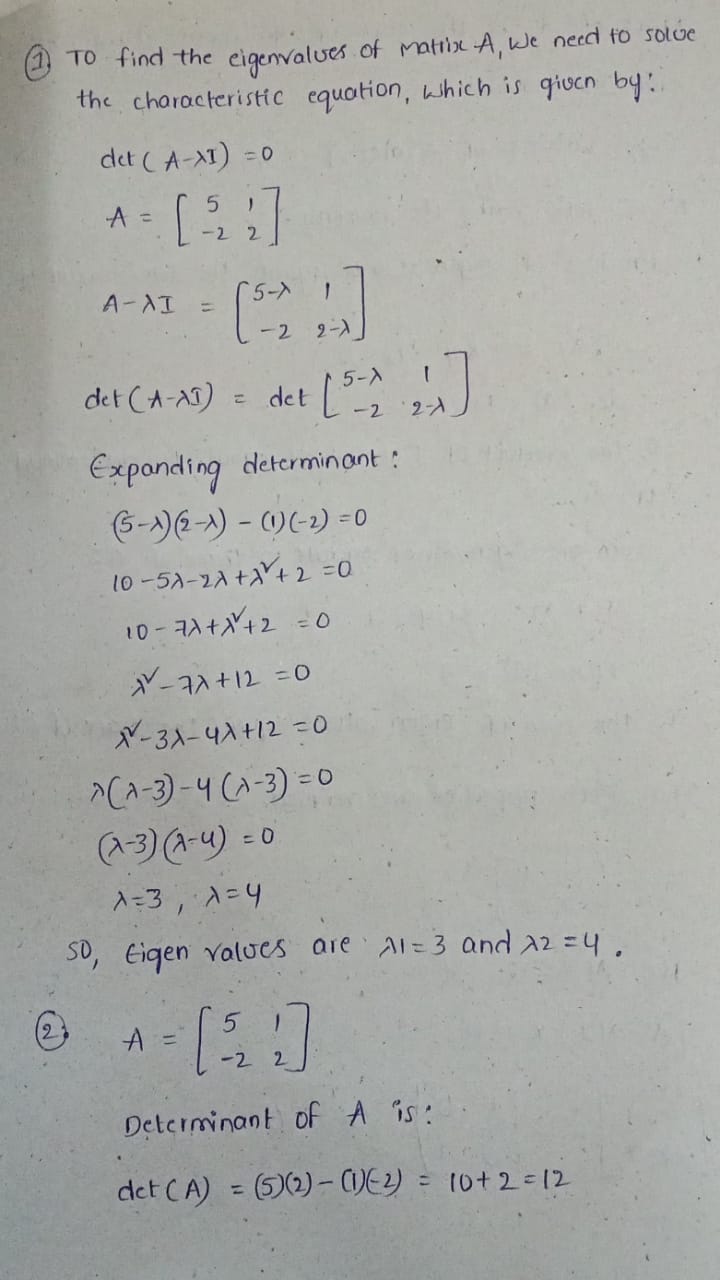
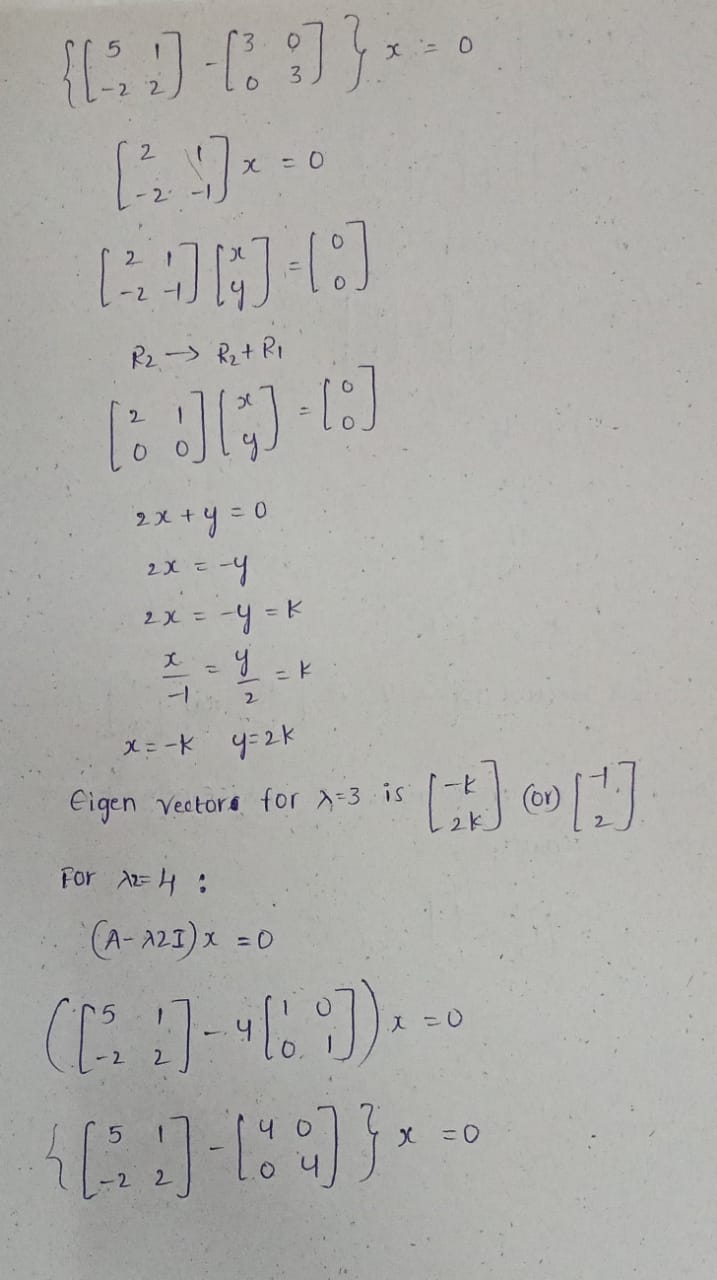
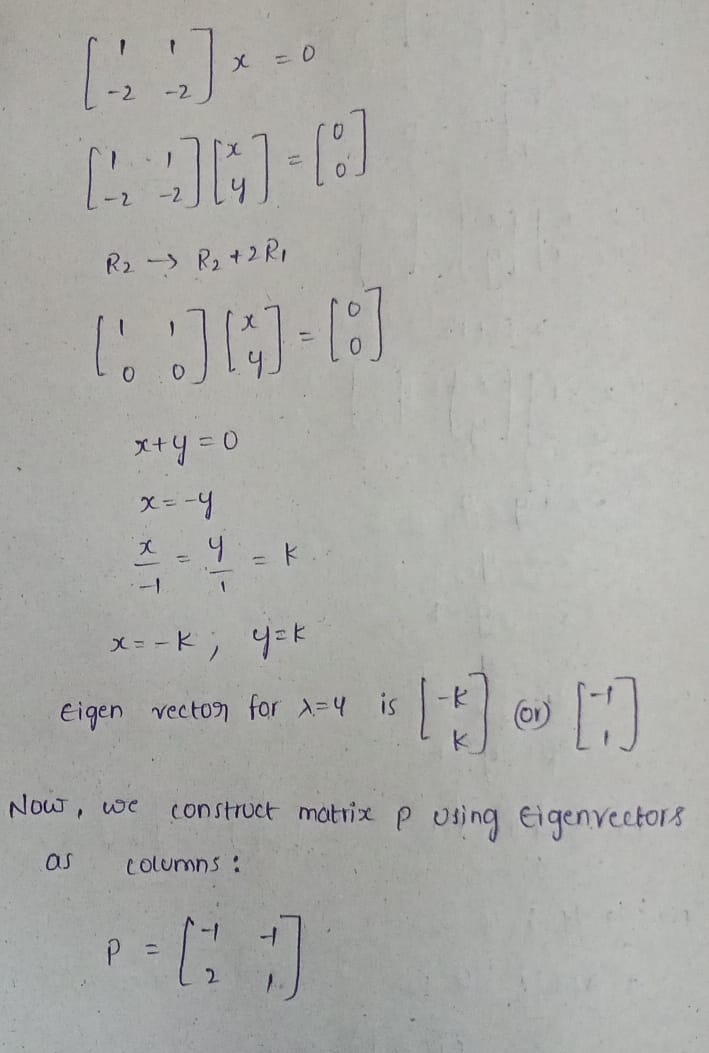
51] Use the matrix: A= [_2 ) 1. Determine the eigenvalues of A by solving the characteristic equation. 2. Verify that the product of the eigenvalues is equal to the determinant of 4, and the sum of the eigenvalues is equal to the trace of A. 3. Determine the matrix P whose columns are the eigenvectors of 4. To find the eigenvalues of matrix A, We need to solve the characteristic equation, which is given by: det ( A- X I ) = 0 A = [ 52 2] A-NI = 15- 7 1 - 2 2 -7 det (A-AT ) = det / 5-2 1 - - 2 2 -4 Expanding determinant ? ( 5- 1 ) ( 2- 1 ) - (1) ( - 2 ) = 0 10-52-27 + 2 +2 =0 10- 71+* +2 =0 AV - 72 + 12 = 0 1- 34 - 4* + 12 = 0 ( A-3 ) - 4 ( 1 - 3 ) = 0 ( 2 - 3 ) ( 7 - 4 ) = 0 1= 3 , 1 = 4 So, Eigen values are 21= 3 and 22=4. A Determinant of A is : det ( A) = (5) (2) - (1) ( 2) = 10+ 2= 12Trace of A is the sum of diagonal elements: Trace (A) = 5+2 = 7 Eigen values of A are >1 = 3 and 12 = 4 Now, let's verify the properties : 1. Product of eigen values equals the determinant of A : *1 . 12 = 3 * 4. = 12 det CA ) = 12 So, the product of eigenvalues equals to determinant of A. 2. Sum of eigenvalues equals to trace of A: Al + 12. = 3+ 4 = 7 Trace ( A) = 7 so, the sum of eigen values equals the trace of A. Thus, Both properties are verified. 3 A = [5 1] for 21 = 3 : (A - NI ) X = 0 1 = 012 1 7 x = 0 R2 - > RX+ RI 2 x + 4 = 0 2X = - 4 2 X = - 4 =K L = 1 = K 2 X = - * 4= 2k Eigen Vectors for 2= 3 is For AZH : (A-AZI ) X = 0 x = 0X = 0 R 2 -3 R 2 + 2 RI ! ! : 71:] = 18] x+ 4 = 0 x = -y x - 9 =K x = - K; y=k Eigen vector for >= 4 is [ -k ( [:) Now, we construct matrix p using Eigenvectors as columns : P