5.3) MATLAB Exercises 1. Extend the factorial function defined above, such that it checks for a positive input argument. 2. Write a function that calculates a random walk trajectory based on the iteration xi+1 = xi + , where is a uniformly distributed random variable between -1 and 1. Plot the resulting trajectory. 3. Change the sorting algorithm given below such that it sorts the elements in descending order. Compare the speed of your function with the built-in MATLAB function sort.

4. Approximation of . The area of a circle is given by A = r^2 where r is the radius. Assume a circle with r = 0.5 embedded in a unit square. A point in the unit square is defined by p = (x,y) where 0 x,y 1. If we draw ntot times two uniformly distributed random numbers (x,y) and count how often the corresponding points falls into the circle (ncirc), we get an approximation of the circle area by ncirc tot and by that of the number . Write a function which approximates by the described method. How many draws do you need to get the rst three digits right?

Note: part 3 to 4 missing (Please answer the two remaining parts). I forgot to put on instructions on part 2 maybe that changes everything. For some reason the symbol didn't transfer over here on text but I manage to fixed now. I manage to add the sorting algorithm example in part 3 below but it needs to be change in descending order and compare the speed of your function with the built-in MATLAB function sort..

My answer part 1)

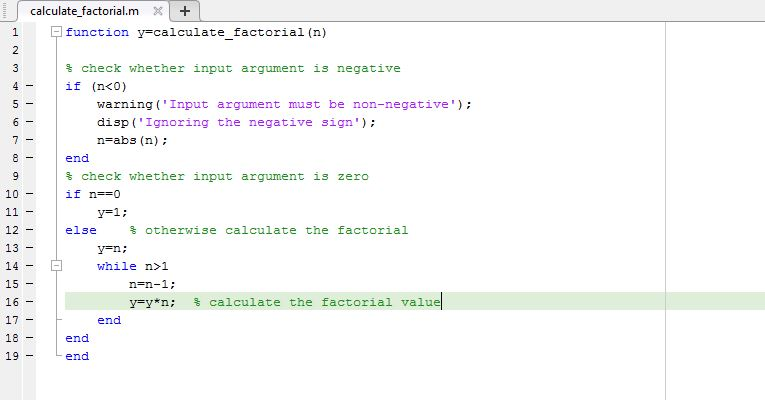
function y=calculate_factorial(n)

% check whether input argument is negative if (n1 n=n-1; y=y*n; % calculate the factorial value end end end

SCREENSHOT OF CODE:

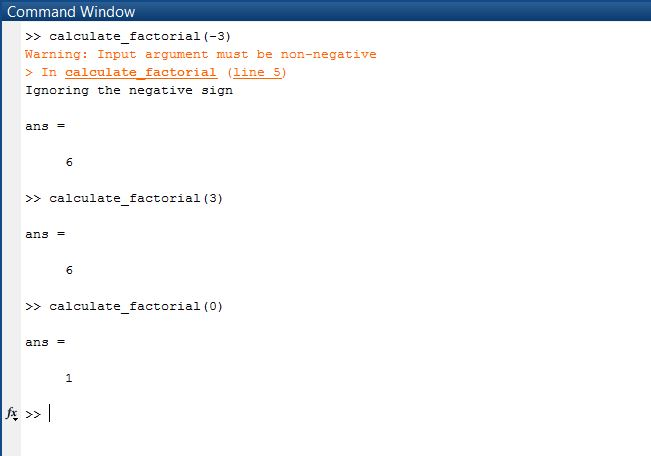
SAMPLE OUTPUT:

part 2)

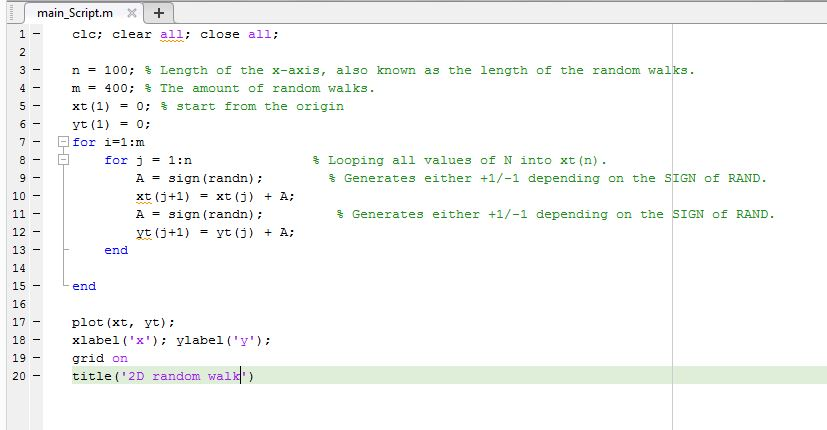
clc; clear all; close all;

n = 100; % Length of the x-axis, also known as the length of the random walks. m = 400; % The amount of random walks. xt(1) = 0; % start from the origin yt(1) = 0; for i=1:m for j = 1:n % Looping all values of N into xt(n). A = sign(randn); % Generates either +1/-1 depending on the SIGN of RAND. xt(j+1) = xt(j) + A; A = sign(randn); % Generates either +1/-1 depending on the SIGN of RAND. yt(j+1) = yt(j) + A; end end

plot(xt, yt); xlabel('x'); ylabel('y'); grid on title('2D random walk')

=============================== SCREENSHOT OF CODE

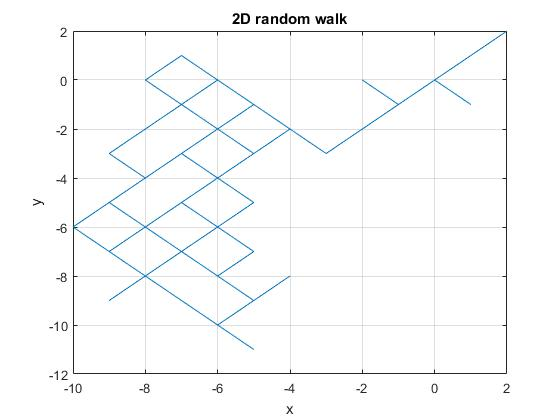
============================================ SAMPLE OUTPUT

Example for part 3 needs to be change in descending order the example below is in ascending order: the following function sorts the elements of a vector in ascending order. function v = gsort(v)

pos = 2;

while pos v(pos-1) % move to the next position

pos = pos + 1;

else % swap the values

foo = v(pos-1);

v(pos-1) = v(pos);

v(pos) = foo;

if pos > 2 % decrease position

pos = pos - 1;

end

end

end

calculate factorial.m+ function y=calculate factorial (n) check whether input argument 13 negative warning ('Input argument must be non-negative'): disp'Ignoring the negative sign) n=abs (n) ; end % check whether input argument is zero if n 0 10 Y-1: 12else 13 % otherwise calculate the factorial y=n; while 15 16 n>1 n-n-1: y=y*n; % calculate the factorial value end end end Command Window > calculate factorial (-3) Warning: Input argument must be non-negative > In calculate factorial (line 5) Ignoring the negative sign ans - >> calculate_factorial (3) ans - >> calculate_factorial (0) ans - fx >> main_Script.m+ clc: clear all: close all: n = 100; % Length of the x-axis, also known as the length of the random walks. m 400; % The amount of random walks. xt (1) % start from the origin yt (1) = 0; for i-1:m 4- for 1 : n % Looping all values of N into xt (n) . % Generates either +1/-1 depending on the SIGN of RAND A 3ign (randn) ; xt(j+1) = xt (j) + A; A = 3ign (randn) ; 10 % Generates either +1/-1 depending on the SIGN of RAND 12 13 14 end end 16 17 plot (xt, yt); x1abe1 ( x' ) ; ylabel ( 'y') ; grid on title ('2D random wall) 20 2D random walk 2 -2 -4 -6 -8 -10 -12 -6 -2 2 -10 -8