Question: 6. For each relation on R, decide whether the relation is reflexive, symmetric, antisymmetric, and transitive. No justification required if yes but provide example if

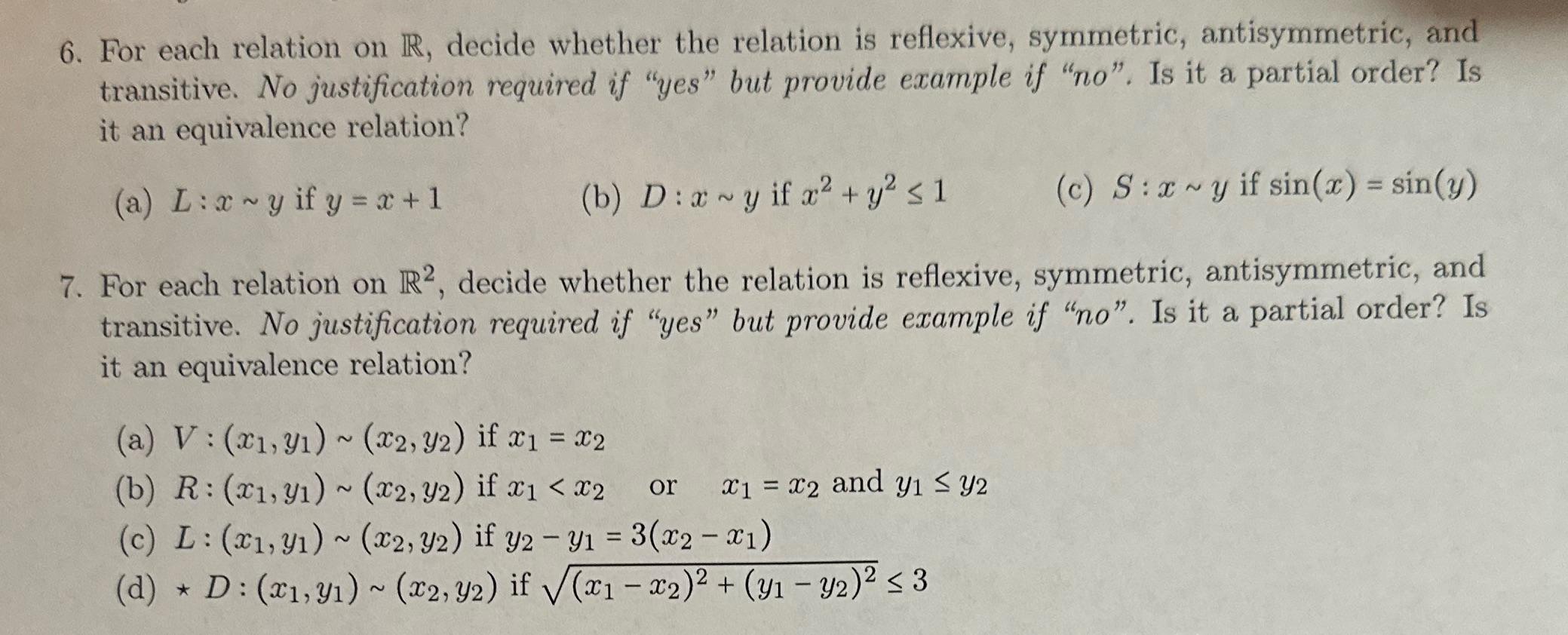
6. For each relation on R, decide whether the relation is reflexive, symmetric, antisymmetric, and transitive. No justification required if "yes" but provide example if "no". Is it a partial order? Is it an equivalence relation? (a) L :x~ yify = x+1 (b) D : x~ y ifa2 +y's1 (c) S : x ~ y if sin(x) = sin(y) 7. For each relation on R2, decide whether the relation is reflexive, symmetric, antisymmetric, and transitive. No justification required if "yes" but provide example if "no". Is it a partial order? Is it an equivalence relation? (a) V : (x1, y1) ~ (x2, 32) if x1 = 22 (b) R: (21, y1) ~ (x2, y2) if x1

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Sometimes we write a ~ b instead of (a, b) E R. In this notation, a relation ~ on a set X is Reflexive "D~DX DA J! Symmetric 'D ~ q + q ~D q X > q'DA J! Antisymmetric if Va, bEX a~ bAb~ a - a= b....

This is a C programming assignment. (and about discrete math) Write an algorithm to draw Hasse diagram of the given relations in "relations.txt". . Read the relations in the text file"...

Problem 2 For the problems 5a to 5c, determine whether the relation R on the set of integers is reflexive, symmetric, antisymmetric, and/or transitive, where (x, y) ? R if and only if a) x + y = 0....

You can implement your algorithm in C programming Write an algorithm to draw Hasse diagram of the given relations in input.txt Your code should meet the following requirements, standards and...

Determine whether relation R on the set of all integers is reflexive, symmetric, antisymmetric, and/or transitive. R={(a,b)bismultipleofa} 10. Relation R is represented by the matrix MR=101010111....

Math 221 Discrete Mathematics UOPX Make sure all of the are fresh work with proper citation APA format, no used work will be accepted thanks so much. To be substantive, in addition to meeting the...

a) Consider the following relation R on the set {x, y, z, v}: R = (x, x),(x, y),(x, z),(x, v),(y, y),(y, z),(y, v),(z, z),(z, v),(v, v),(v, z) . Determine whether R is reflexive, transitive, a...

undefined 6. (a) Consider the following relation R on the set {x,y,z, v}: R= {(x,x), (x,y),(2, 2), (2, v),(y,y),(y,x),(4,0), (2, 2), (2, 4), (u, v), (0, 2)}. Determine whether R is reflexive,...

4.Determine whether the following binary relations are reflexive, symmetric, antisymmetric and transitive: a. x R y xy 0 x, y R b. x R y x > y x, y R c. x R y |x| = |y| x, y R For each of the above,...

For each of the following relations on the set specified, determine whether the relation is reflexive, symmetric, antisymmetric, or transitive. Also determine whether it is a partial order or an...

Aubergine Corporation uses the periodic inventory system to record its inventory. The following information was available for the month of November: Date...

You were provided with the following balance sheet for Golden Cup firm for the year ended Dec 31 st , 2018. Consolidated Balance sheet Golden Cup. As of Dec 31 st , 2018 Assets Liabilities + Owners...

When considering expected returns, the states of the world must sum to 1 ( or 1 0 0 % ) . Group of answer choices True False

need held on this operation -/5 Question 17 of 35 View Policies Current Attempt in Progress During 2022 Nash's Trading Post, LLC had sales On account of $700000, cash sales of $300000, and...