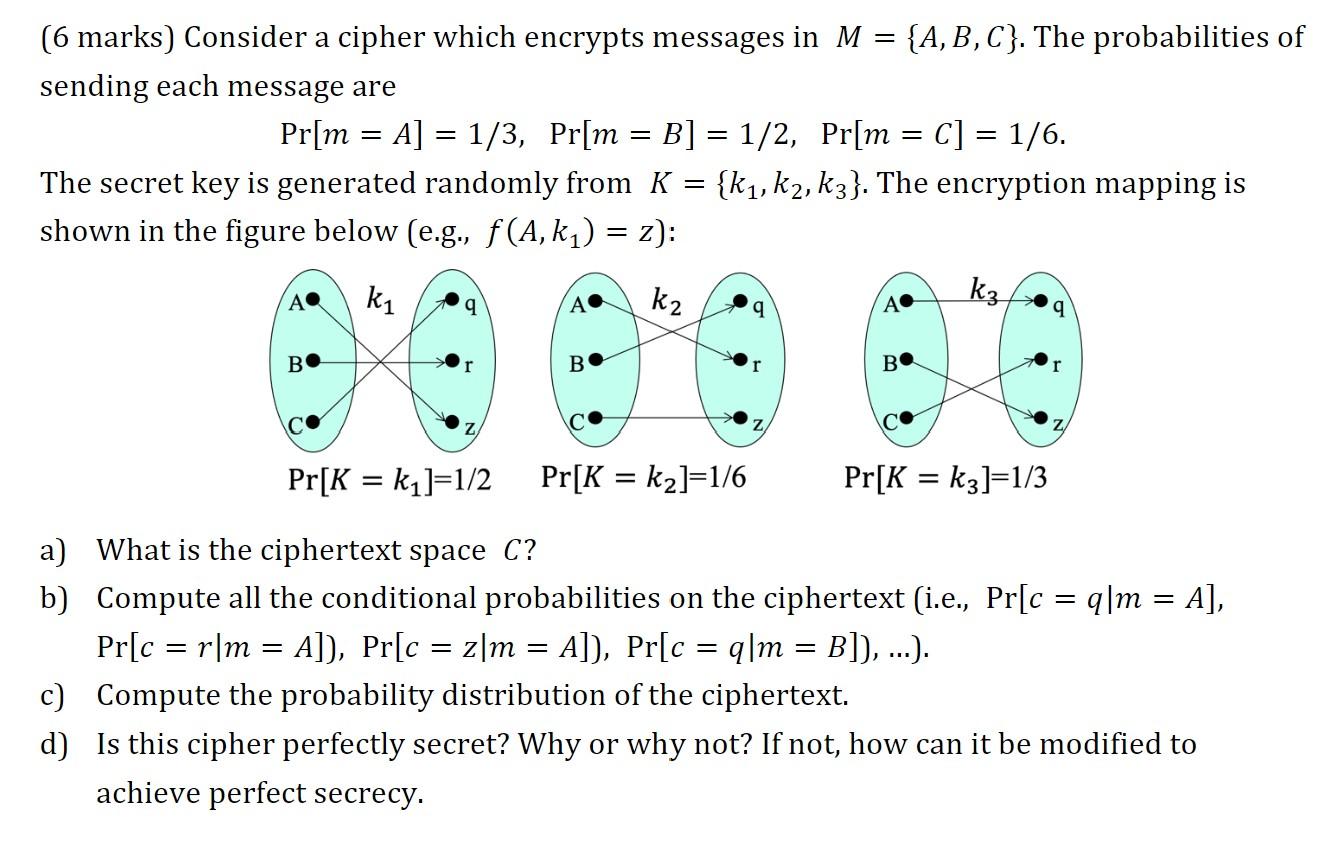
(6 marks) Consider a cipher which encrypts messages in M = {A,B,C}. The probabilities of sending each message are Pr[m = A] = 1/3, Pr[m = B] = 1/2, Pr[m = C] = 1/6. The secret key is generated randomly from K = {k, k2, k3}. The encryption mapping is shown in the figure below (e.g., f(A, k) = z): = = = k k3 q A kz q A q BO B BO r Pr[K = k1]=1/2 = - Pr[K = k2]=1/6 Pr[K = kz]=1/3 = = = = = = = = = a) What is the ciphertext space C? b) Compute all the conditional probabilities on the ciphertext (i.e., Pr[c = q m = A], Pr[c = r[m = A]), Pr[c = z[m = A]), Pr[c =q|m = B]), ...). c) Compute the probability distribution of the ciphertext. d) Is this cipher perfectly secret? Why or why not? If not, how can it be modified to achieve perfect secrecy