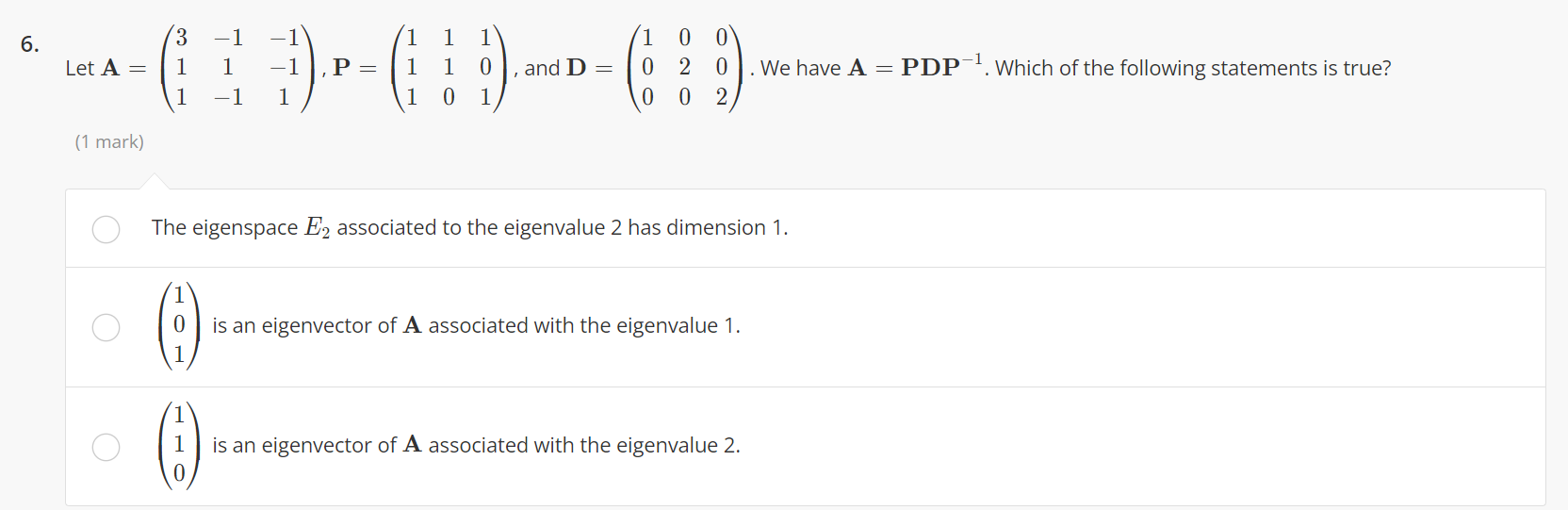
Question: 6. NO Let A = 1 P 1 0 , and D = NOO We have A = PDP . Which of the following statements

Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


