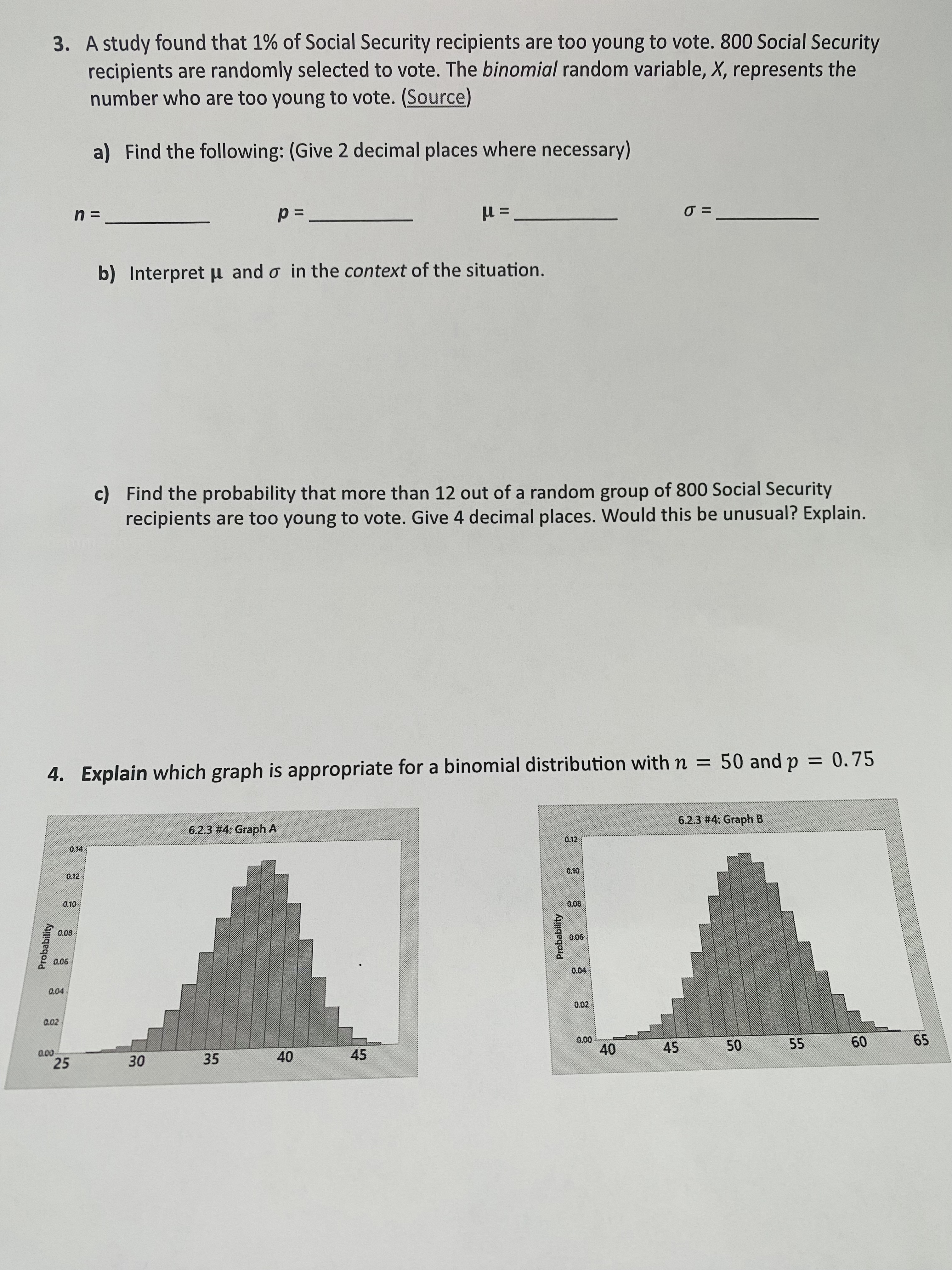
6.2: Binomial Distribution 1. Determine whether or not following probability experiments qualify as a binomial experiment. For those that are binomial experiments, identify and/or explain n, S, F, X, p and q. For those that are NOT binomial experiments, explain why not. a) Meijer asks 450 random customers whether they \"enjoyed their shopping experiences at Meijer?\" Customers choose from three possible responses, \"yes\3. A study found that 1% of Social Security recipients are too young to vote. 800 Social Security recipients are randomly selected to vote. The binomial random variable, X, represents the number who are too young to vote. (Source) a) Find the following: (Give 2 decimal places where necessary) "2 p: '1: 0': b) Interpret u and 0' in the context of the situation. c) Find the probability that more than 12 out of a random group of 800 Social Security recipients are too young to vote. Give 4 decimal places. Would this be unusual? Explain. 4. Explain which graph is appropriate for a binomial distribution with n = 50 and p = 0.75 5. 13.6% of the U.S. population is foreign-born. You are going to select 50 unrelated, random people in the U.S. (Give 4 decimal places and P(X) notation from StatCrunch) (Source) a) State n: and p: b) Find the probability that at most 5 of the people are foreign-born. c) Find the probability that at least 8 of the people are foreign-born. d) Find the probability that between 2 and 7, inclusive, of the people are foreign-born. e) Find the probability that none of the people in the sample are foreign-born. Would this be unusual? Explain. f) Find the mean and standard deviation of this binomial experiment g) Interpret the mean and standard deviation in the context of the situation. Be specific