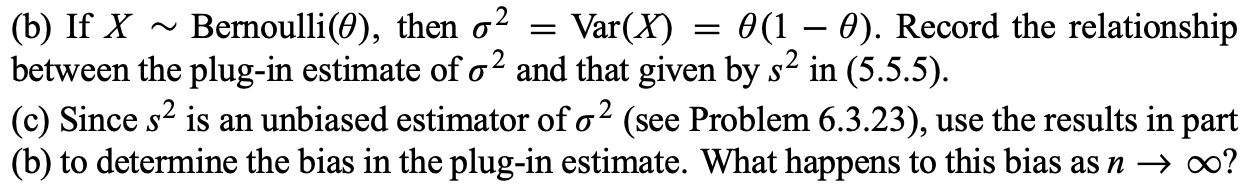
6.3.13 Suppose (x1,..., xn) is a sample from a Bernoulli() with [0, 1] unknown. (a) Show that -n i=1(xi x)2 = nx(1 x). (Hint: x2 i = xi .)

(b) If X Bernoulli( ), then 2 = Var(X) = (1 ). Record the relationship between the plug-in estimate of 2 and that given by s2 in (5.5.5). (c) Since s2 is an unbiased estimator of 2 (see Problem 6.3.23), use the results in part (b) to determine the bias in the plug-in estimate. What happens to this bias as n ?

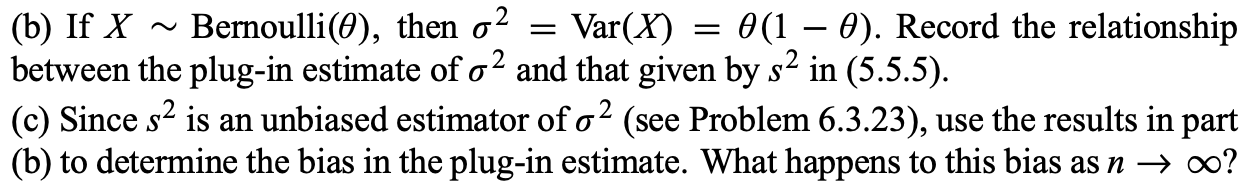
\f(b) If X N Bemoulli(6), then 02 = Var(X) = 6(1 6). Record the relationship between the plug-in estimate of 0'2 and that given by 32 in (5.5.5). (0) Since 32 is an unbiased estimator of 02 (see Problem 6.3.23), use the results in part (b) to determine the bias in the plug-in estimate. What happens to this bias as n ) oo