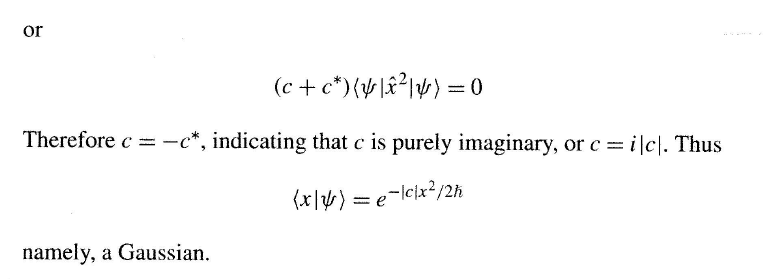
6.7. In Example 6.2 it was assumed that (px) = 0. Determine the minimum uncer- tainty wave function if this constraint is relaxed. EXAMPLE 6.2 Use the results of Section 3.5 to prove that the wave func- tion for which Ax Apx = /2 must be a Gaussian. SOLUTION In Section 3.5 we established the general uncertainty relation AAAB |(C)|/2 for observables A and B for which the corresponding operators satisfied the commutation relation [A, B]=i. The derivation started with the Schwarz inequality (ala) (BB) |(aB) | with a) = ( (A))|) and B) = (B - (B)). For AAAB= |(C)|/2 to hold, there are two requirements. One is that [B) = cla), where c is a constant, so that the Schwarz inequality becomes an equality and (||v) = 0, where = + * with = ( (A))(B (B)). We can simplify things a bit by positioning the origin so that (x) = 0 and choosing a frame of reference for which (px) = 0. Then the two requirements become and cx|v) = Px|v) ((Px + x)) = 0 Projecting the first equation into position space, we see that a(x|v) i x which has the solution cx (x|y) = (x|y) = eicx/2h The first requirement also shows us that (v|px = c* (v|x Using these results in the second requirement, we see that (v|(xcx + c*xx) | y) = 0 or (c +c*) (v|x|v) = 0 Therefore c = -c*, indicating that c is purely imaginary, or c = i|c. Thus (x|v) = e-\c\x/2h namely, a Gaussian.