Question: 7. (3) Let S1(0) = {r L2(0, 1)|||| = 1}. Prove that S1(0) is closed. Prove that a continuous (not necessarily linear) function f

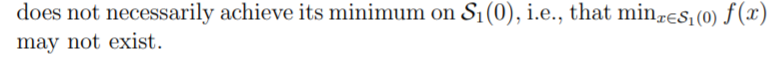
7. (3) Let S1(0) = {r L2(0, 1)|||| = 1}. Prove that S1(0) is closed. Prove that a continuous (not necessarily linear) function f

7. (3) Let S1(0) = {r L2(0, 1)|||| = 1}. Prove that S1(0) is closed. Prove that a continuous (not necessarily linear) function f : S1(0) R does not necessarily achieve its minimum on Si(0), i.e., that min-eS, (0) (x) may not exist.

Step by Step Solution

★★★★★

3.44 Rating (167 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

Solutin x Lelo1 l12l11 and contirues let Silo let that Sico is closed ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Let R. A function f : E R is said to be increasing on E if and only if x1, x2 E and x1

Let f : (a, b) R be continuous on [a, b] and differentiable in (a, b). Show that if then f(a) exists and equals A. [Use the definition of f(a) and the Mean Value Theorem.] im f(x)-A

Let f be a nonnegative continuous function defined on 0 ( x Show that (a) If limx( f(x) exists it must be 0; (b) It is possible that limx( f(x) does not exist. Roa f(x) dx

1. Find all r so that 13r - 1) - |x - 3) = 2x - 1. Prove that you have all solutions. 2. Prove that : 430.is an irrational number 3. Let 21 - v2 and Im VI +,-1. Prove that for all n 2 1, I, is an...

make sure to tackle al (i) According to the Ramsey model, what is the impact of a "fiscal stimulus" on investment, consumption and output if the stimulus is financed with lump-sum taxes? What if it...

"DISCUSS THE EFFECTS OF COVID 19 ON LABOR MARKETS AND THE ECONOMY" Provide an introduction and the background of your study, and clearly state what your research question or objective is. What real...

For the input values of A and B, use the program to determine the value of Y. LET C = A * B IF ((C ( 10) AND (A

Let denote the proportion of voters in a certain state who favor a particular proposed constitutional amendment. Consider testing H 0 : = .5 versus H a : > .5 at significance level .05 based on a...

A study by Triller et al. (A-14) examined the length of time required for home health-care nurses to repackage a patients medications into various medication organizers (i.e., pill boxes). For the 19...

Write the vector F in the cylindrical coordinate system (r, 0, 2) system by defining x = r cos 0, y = r sin 0, and z = z. Note that the vector function in the cylindrical coordinate system is...

DGK Company maintains a lockbox account to facilitate the collection of its accounts receivable. All of the companys cash receipts from credit sales are sent directly to a post office box held in the...

Which of the following characteristics does NOT apply to job order cost accounting? Question 2 options: Use of job cost sheets Aims to compute the cost per individual product Equivalent units of...

Do 2 structures of HCN and their formal charge and use FC to choose the best Lewis structure. Draw 5 different structures and their formal charge analysis of N20 and determine the best Lewis...

(3) Show that the system of quaternions can be represented as a system of real matrices of size 4 x 4.

A boy walks 4.0m East and 3.0 m North. What is his resultant displacement vector? 5.0 m, 37 deg N of E 5.0 m, 37 deg E of N 5.0 m , 37 deg N of W 5.0 m, 37 deg w of N

A ball rolls down in an inclined plane with uniform acceleration of 1.00 m/s. At a certain instant, its velocity is 0.5 m/s. Determine distance travelled by the ball in 10 seconds 55 m O 539.81 m 5.5...

An airplane travels 210 km on a straight course making an angle of 22.5 degrees east of north. it changes its course by moving 110 km N before reaching its destination. Determine the resultant. 304...

What is the measure of DBC? (4 points) 36 72 18 54 In circle A shown below, BD is a diameter and the measure of CB is 36: C 36 B A D

Given the time-phased work packages and network, complete the baseline budget form for theproject. 6 4 10 ESI ID | EF SL LS SL 5 D 10 10 F 12 LF 5 5 10 10 2 12 0 55 Cost by Week A 10 1010 10 B 848 4...

Let S 1 be a causal and stable LTI system with impulse response h 1 [n] and frequency response H 1 (e j ). The input x[n] and output y[n] for S 1 are related by the difference equation y[n] y[n 1]...

Following are the average yields of long-term new corporate bonds over a several-month period published by the Office of Market Finance of the U.S. Department of the Treasury. a. Explore trends in...

Consider a Poisson counting process with arrival rate, . Suppose it is observed that there have been exactly arrivals in [0, t] and let S1, S2 Sn be the times of those arrivals. Next, define X1, X2...

For each set of Stokes parameters given below deduce the amplitude of the electric field, up to an overall phase, in both linear polarization and circular polarization bases and makes an accurate...

Let X and Y have a continuous distribution with joint p.d.f. Compute the covariance Cov(X, Y). + xy for 01 and 0 s y s1 0 otherwise. f(x,y)= t. V