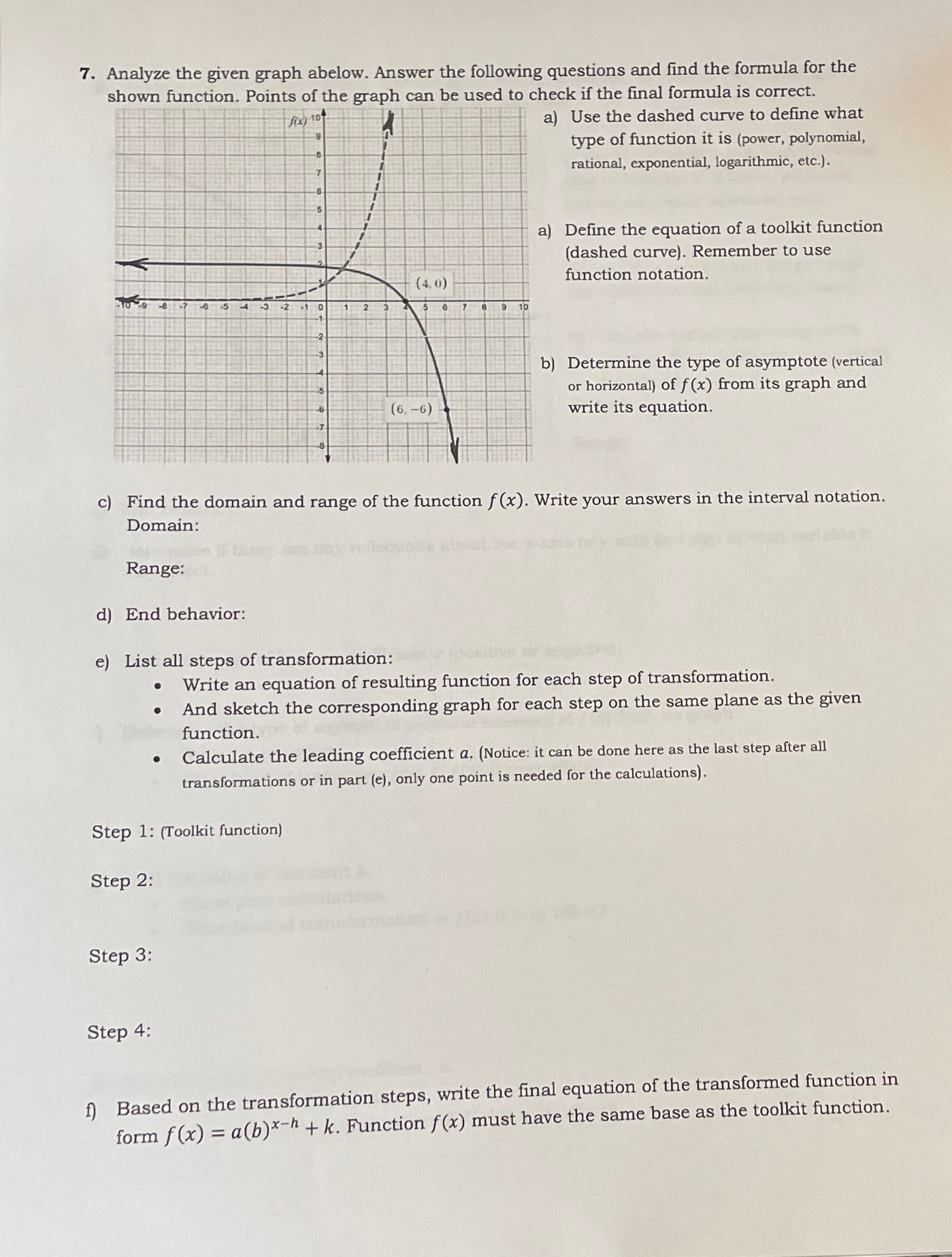
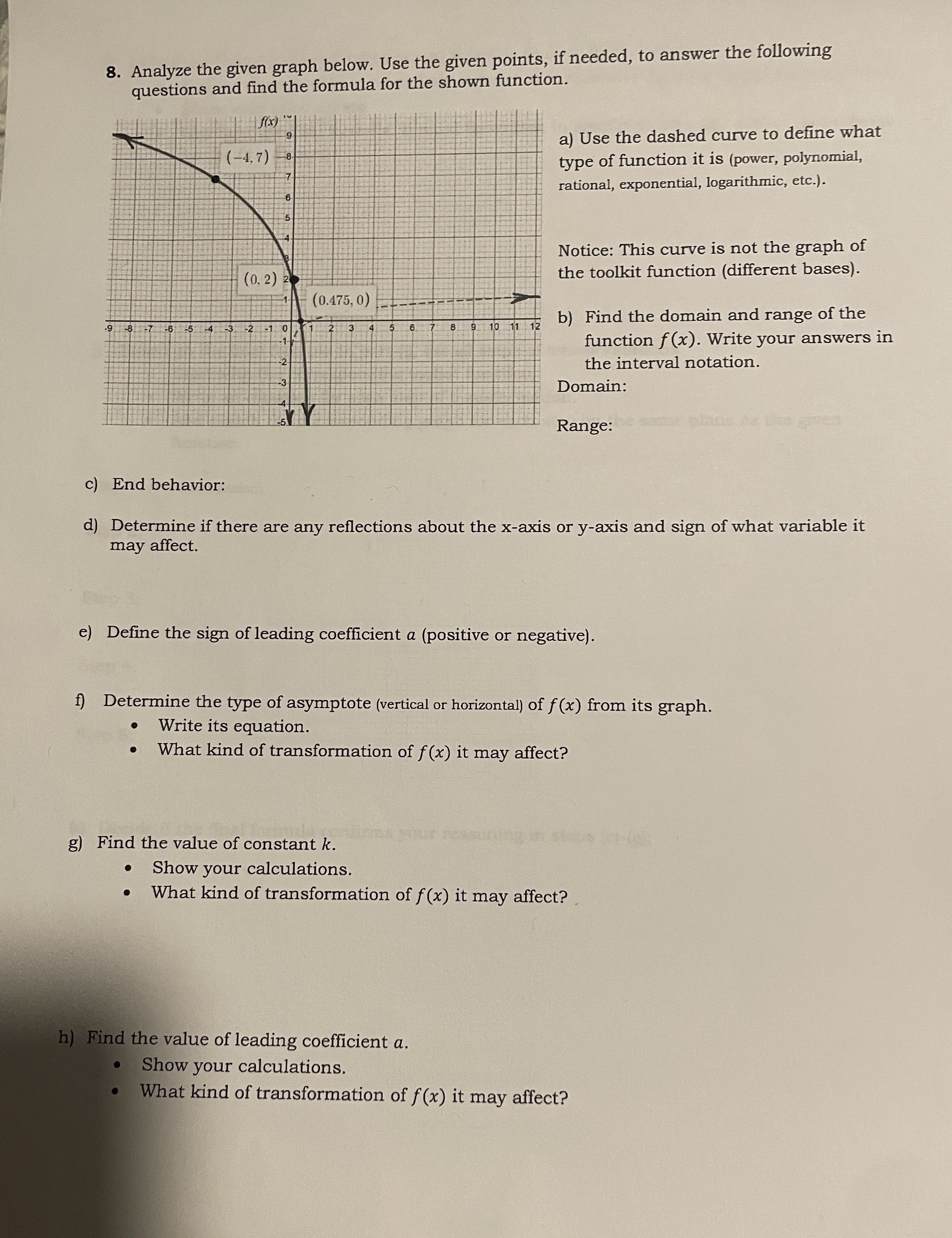
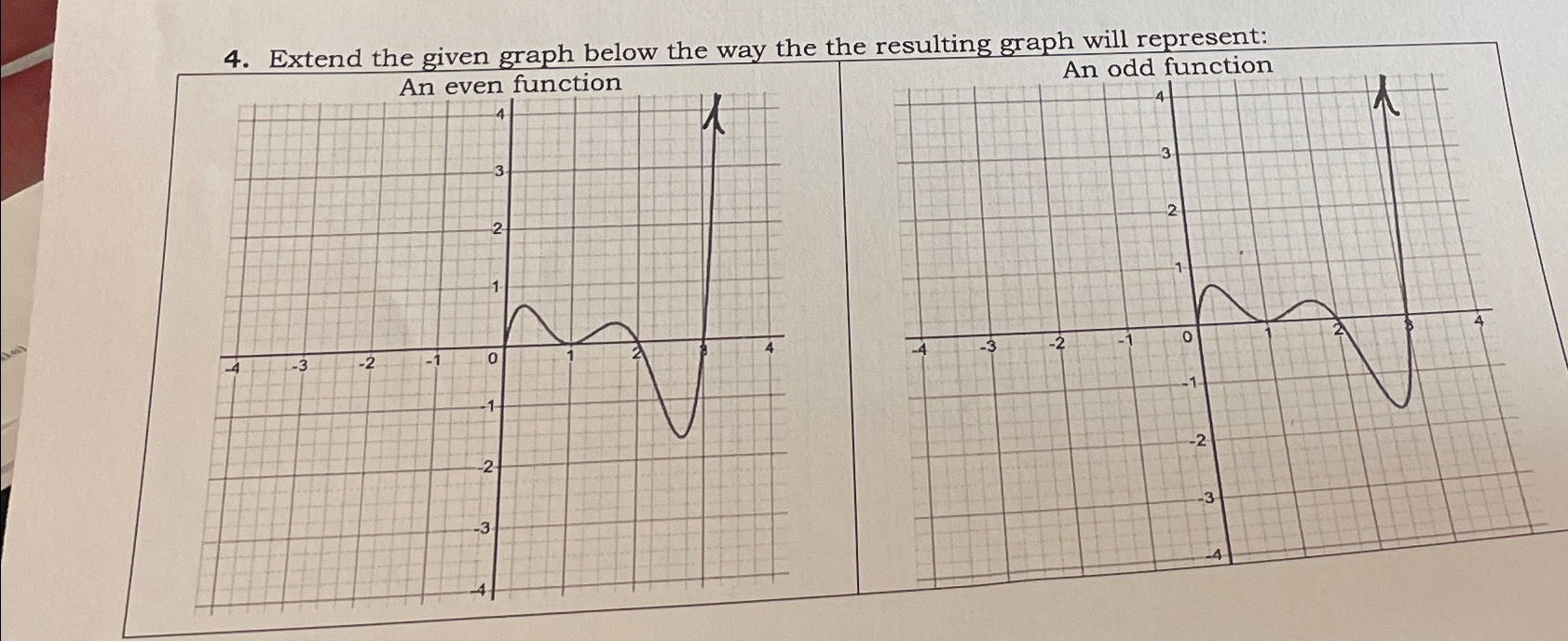
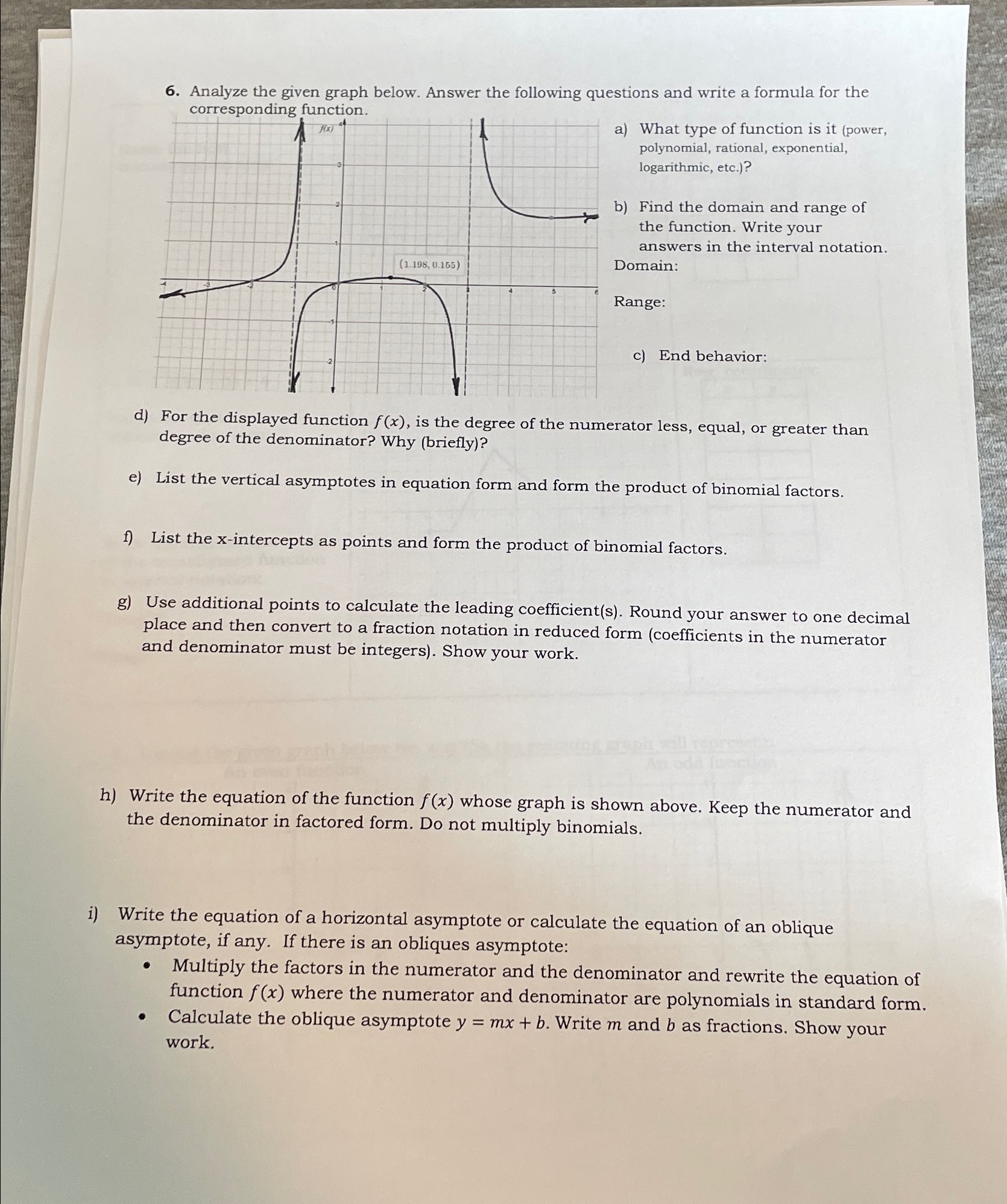
7. Analyze the given graph abelow. Answer the following questions and find the formula for the shown fuTnct:ion. Points of the graph can be used to check if the final formula is correct. 1 e ' Eet . a) Use the dashed curve to define what l i type of function it is (power, polynomial, rational, exponential, logarithmic, etc.). + a) Define the equation of a toolkit function (dashed curve). Remember to use function notation. | b) Determine the type of asymptote (vertical or horizontal) of f(x) from its graph and write its equation. c) Find the domain and range of the function f(x). Write your answers in the interval notation. Domain: Range: d) End behavior: e) List all steps of transformation: Write an equation of resulting function for each step of transformation. And sketch the corresponding graph for each step on the same plane as the given function. Calculate the leading coefficient a. (Notice: it can be done here as the last step after all only one point is needed for the calculations). transformations or in part (}, Step 1: (Toolkit function) Step 2: Step 3: Step 4: write the final equation of the transformed function in Based on the transformation steps, - . 2 f(x) must have the same base as the toolkit function. form f(x) = a(b)*~" + k. Function i) Define the final equation of transformed function in form f(x) = alogb (x - h) + k. Use the change-of-base formula to convert from common log to the log of different base. Show your calculations. Highlight the final formula. It must be written in simplified form (no double parenthesis for the (x - h) part). j) Based on the final formula in part (i), list all steps of transformations Start with the corresponding toolkit function Write an equation for each step of transformation. And sketch the corresponding graph for each step on the same plane as the given function. Step 1: (Toolkit function) Step 2: Step 3: Step 4: Step 5: k) Decide if the final formula confirms your reasoning in steps (c)-(g):f ' S 8. Analyze the given graph below. Use the given points., if needed, to answer the following . quesions and find the formula for the shown function. a) Use the dashed curve to define what - type of function it is (power, polynomial, rational, exponential, logarithmic, etc.). Notice: This curve is not the graph of the toolkit function (different bases). b) Find the domain and range of the function f(x). Write your answers in the interval notation. Domain: ,. g O L b L iy ! Range: c) End behavior: d) Determine if there are any reflections about the x-axis or y-axis and sign of what variable it may affect. e) Define the sign of leading coefficient a (positive or negative). f) Determine the type of asymptote (vertical or horizontal) of f(x) from its graph. o Write its equation. e What kind of transformation of f(x) it may affect? g) Find the value of constant k. e Show your calculations. What kind of transformation of f(x) it may affect? ue of leading coefficient a. your calculations. kind of transformation of f(x) it may affect? 4. Extend the given graph below the way the the resulting graph will represent: An even function An odd function 3 -2- 2 4 -3 -2 1-1 0 -3 -2 0 2 N -26. Analyze the given graph below. Answer the following questions and write a formula for the corresponding function. 4 e o a) What type of function is it (power, polynomial, rational, exponential, logarithmic, etc.)? b) Find the domain and range of the function. Write your answers in the interval notation. Domain: 1 i | | T | | | | 1 f (1.198,0.165) I Range: c) End behavior: d) For the displayed function f(x), is the degree of the numerator less, equal, or greater than degree of the denominator? Why (briefly)? e) List the vertical asymptotes in equation form and form the product of binomial factors. 1) List the x-intercepts as points and form the product of binomial factors. g) Use additional points to calculate the leading coefficient(s). Round your answer to one decimal place and then convert to a fraction notation in reduced form (coefficients in the numerator and denominator must be integers). Show your work. h) Write the equation of the function f(x) whose graph is shown above. Keep the numerator and the denominator in factored form. Do not multiply binomials. i) Write the equation of a horizontal asymptote or calculate the equation of an oblique asymptote, if any. If there is an obliques asymptote: Multiply the factors in the numerator and the denominator and rewrite the equation of function f(x) where the numerator and denominator are polynomials in standard form. Calculate the oblique asymptote y = mx + b. Write m and b as fractions. Show your work