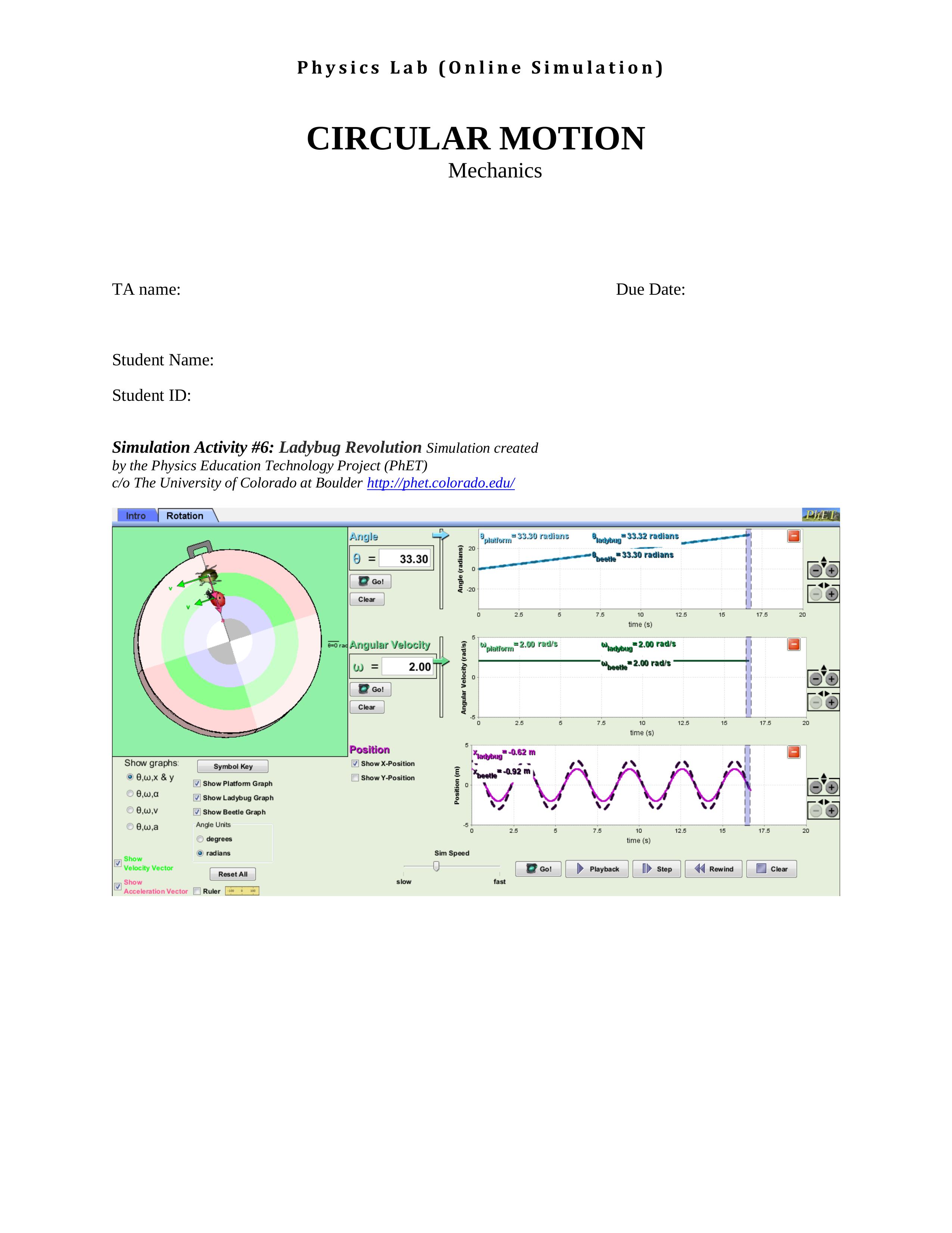
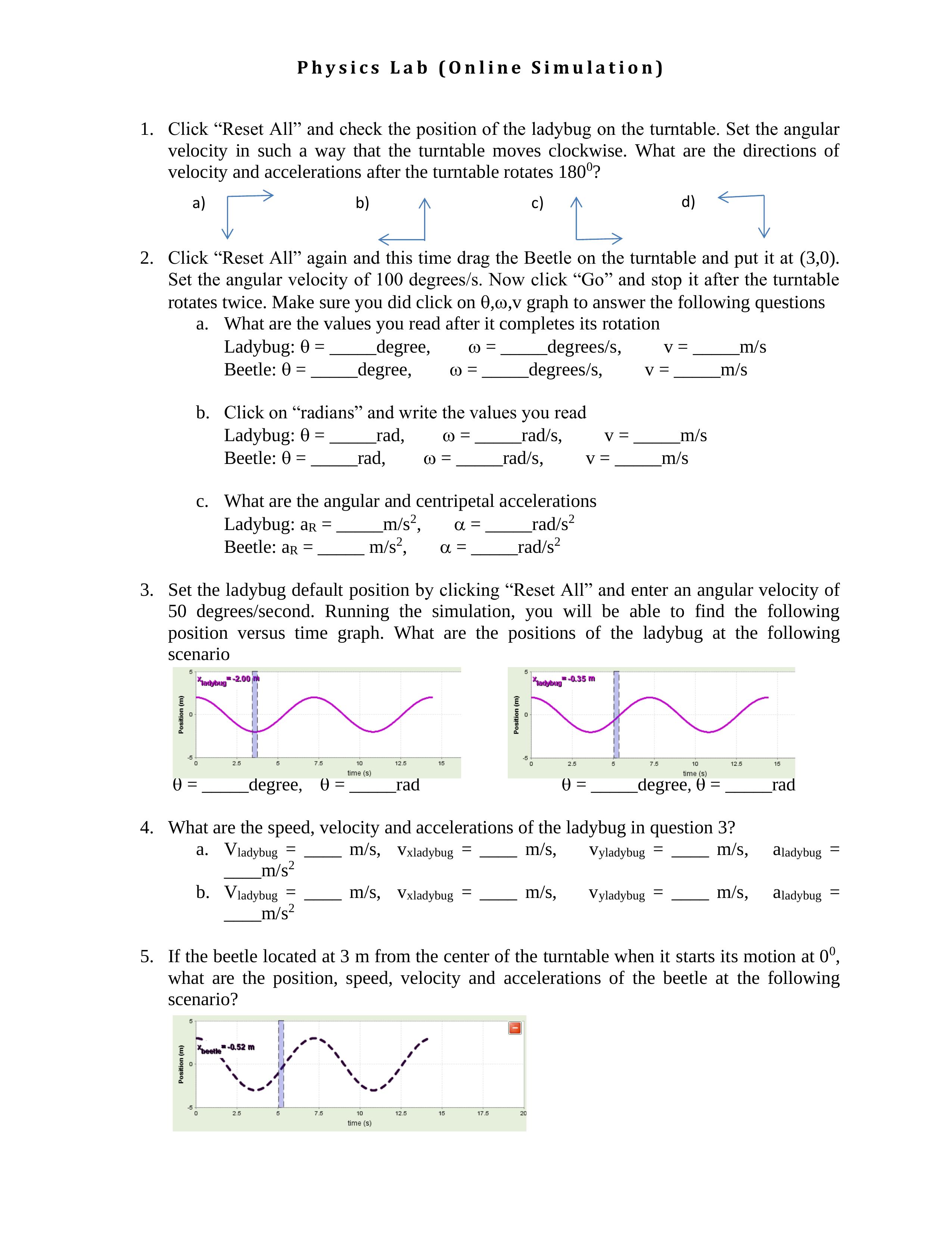
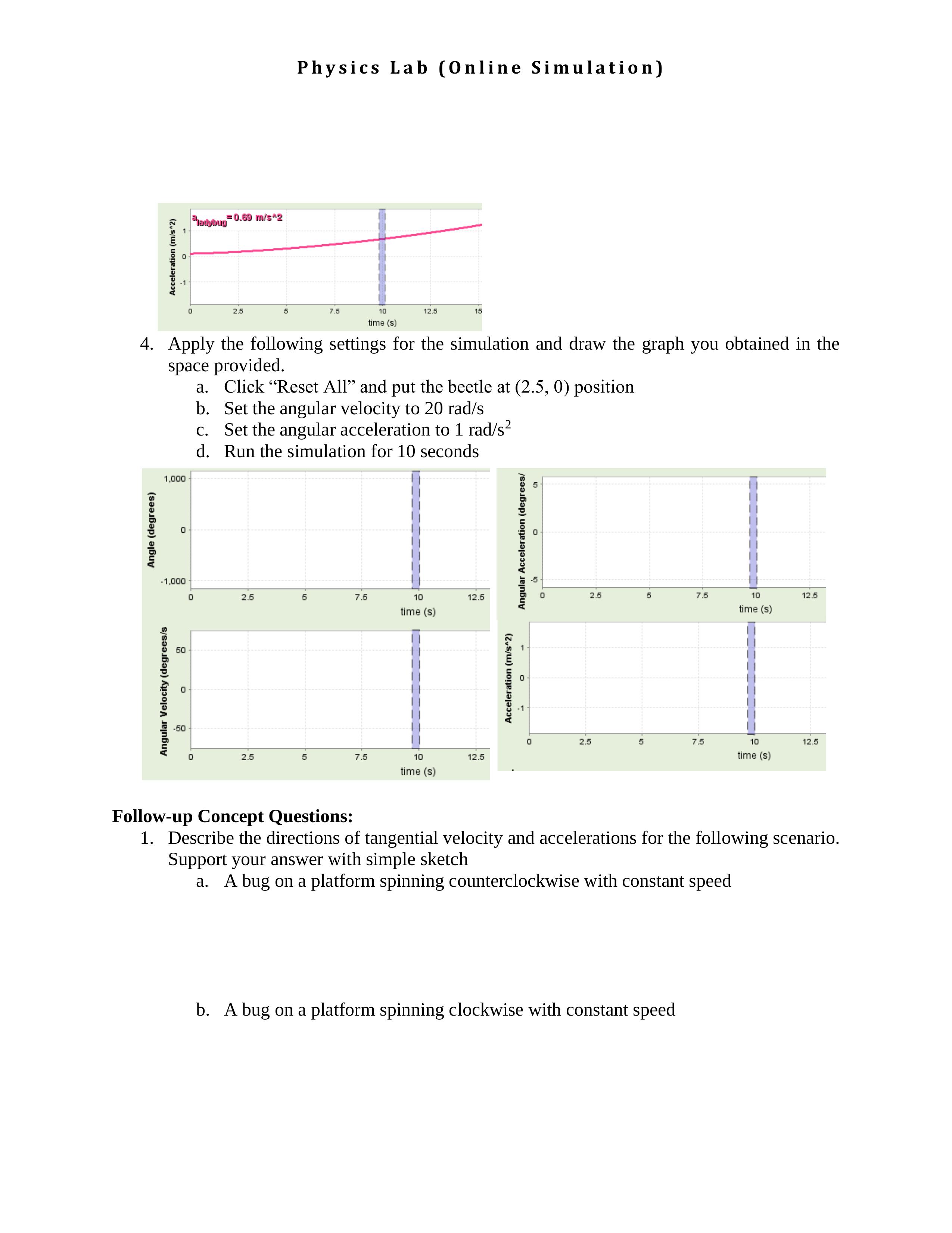
Physics Lab (Online Simulation) CIRCULAR MOTION Mechanics TA name: Due Date: Student Name: Student ID: Simulation Activity #6: Ladybug Revolution Simulation created by the Physics Education Technology Project (PhET) clo The University of Colorado at Boulder http://phet.colorado.edu/ Intro Rotation PHET Angle platform # 33.30 radians hadyoung # 33.32 radians = e 33.30 beetle = 33.30 radians Angle (radians) Go! Clear 25 7.5 10 12.5 17.5 20 time (s 8=0 rac Angular Velocity plation= 2.00 rad/s ladybug 2.00 rad/s W = 2.00 @beetle 2.00 radis Angular Velocity (radis) O'O Go! Clear .5 7.5 12.5 16 17.5 20 ime (s) Position "ladybug -0.62 m Show graphs: Symbol Key Show X-Position 0,W,x & y Show Platform Graph Show Y-Position Position (m O'O O e,w,a Show Ladybug Graph e, w, v Show Beetle Graph 0,w,a Angle Units degrees time (s ) radians Sim Speed show Velocity Vector Reset All Go! Playback I Stop 4 Rewind Clear Show slow fast Acceleration Vector RulerPhysics Lab (Online Simulation) Intro Rotation PKET Angle 20 platform = 12.88 radians ladybug=12.90 radians - D = 12.88 beetle = 12.88 radians Angle (radians) O'O Go! Clear 7.5 10 12.5 15 17.5 20 time (s) 8=0 rac Angular Velocity "platform 5.08 radis waddyburg 5.08 rad/s 0 = 5.08 beetle # 5.08 rad/s Angular Velocity (radis) Go! Clear 7.5 12.5 17.5 time (s) Platform Ang Accel "platform= 1.00 rad/she ladybug = 1.00 rad/s*2 Show graphs: Symbol Key 0, W,X & y 1.00 "beetle = 1.00 rad/s^2 Show Platform Graph Angular Acceleration (radis" . e, w,a Show Ladybug Graph Go! OB, W, v Show Beetle Graph Clear 0,w,a Angle Units 2.5 7.5 12.5 17.5 20 degrees time (s Sim Speed Show radians Velocity Vector Reset All Go! Playback | Step 4 Rewind Clear Show Acceleration Vector Ruler . Investigating Rotational Motion: Angular kinematics and relating angular to linear quantities. Objective: This activity is intended to enhance your physics education. We offer it as a virtual lab online. We think it will help you make connections between predictions and conclusions, concepts and actions, equations and actual motions. We also think that if you give this activity a chance, it will be fun! This is an opportunity to learn a great deal. Answer all questions as you follow the procedure in running the simulation. Join the ladybug and beetle in an exploration of rotational motion. It is possible to determine the angular and linear quantities which can describe the motion of a ladybug on the turning table. All features you need for this simulation can be found on the display by clicking the "Rotation" tab. Graph Type: Click one of the types of graphs among the four types under the "Show graphs". If you couldn't recognize the symbols, click "Symbol Key" Graph Selector: There are three boxes to check and select from. To display graphs which represent the motion of the platform (the turning table), check the "Show Platform Graph" box. Checking this box also helps you to enter values of angular quantities. The other two boxes are used to add position, velocity, and acceleration of the ladybug and/or Beetles. Position: You can place the ladybug and/or Beetle on the platform. The position can be measured using the ruler by checking the "Ruler" box. Vectors: you can check the boxes at the bottom left corner to display the vectors on the ladybug and/or Beetles. In addition, you can see the results in both radian and degrees. Whenever you are ready to run the simulation, click "Go". You can control the speed of the simulation using "Sim speed" slide. You can always restart the platform by clicking on "Rewind" and clear the graph by clicking "Clear".Introduction: Physics Lab (Online Simulation] We have seen the kinematics equations for translational motion in \"Kinematics in one dimension\" simulation. In this simulation we are dealing with rotational kinematics. If the motion is pure rotation, the equations can easily be rewritten by changing the translational symbols to rotational. The symbols and the rotational kinematics equations are given below. co=d6/dt 6: (90+?)(tt0) a =dco/dt w=w0+a(tt0) (02 = a)%+255(xxo) a; = AH/At _ 1 _ 2 Translational Angular Displacement X 6 x = 6R Velocity V 0) V: = coR Acceleration a 0c at = orR angle are degrees and radians. Linear quantities can be related to angular quantities as shown in the table to the left. Angular displacement: units used for As you see the figure on the left, the ladybug is located R from the center of axis of rotation. Its tangential velocity (Vt), tangential acceleration (a), centripetal acceleration (aR), and combined (resultant) acceleration (a) are specified. The equation for centripetal and combined accelerations are given by Procedure I - Uniform Circular Motion: Open Ladybug Revolution http://phet.colorado.edu/simulations/sims.php?sim=Ladybug_Revolution Physics Lab (Online Simulation) 1. Click "Reset All" and check the position of the ladybug on the turntable. Set the angular velocity in such a way that the turntable moves clockwise. What are the directions of velocity and accelerations after the turntable rotates 180? a ) b ) c) d ) . Click "Reset All" again and this time drag the Beetle on the turntable and put it at (3,0). Set the angular velocity of 100 degrees/s. Now click "Go" and stop it after the turntable rotates twice. Make sure you did click on 0,w,v graph to answer the following questions a. What are the values you read after it completes its rotation Ladybug: 0 = degree, degrees/s, V = m/s Beetle: 0 = degree, W = degrees/s, V = m/s b. Click on "radians" and write the values you read Ladybug: 0 = rad, rad/s, V= m/s Beetle: 0 = rad, W : rad/s, V = m/s c. What are the angular and centripetal accelerations Ladybug: aR = m/s = rad/s Beetle: aR = m/s, a = rad/s2 3. Set the ladybug default position by clicking "Reset All" and enter an angular velocity of 50 degrees/second. Running the simulation, you will be able to find the following position versus time graph. What are the positions of the ladybug at the following scenario *Hadyoung -200 m ladybug -0.35 m Position (m) Position (m 2.5 12.5 2.5 12.5 = A time (s ) degree, 0 = rad = A degree, 0 = rad 4. What are the speed, velocity and accelerations of the ladybug in question 3? . Vladybug = Vxladybug = m/s, Vyladybug = m/s, aladybug = m/s b. Vladybug = m/S, Vxladybug = m/S, Vyladybug m/s, aladybug m/s2 5. If the beetle located at 3 m from the center of the turntable when it starts its motion at 0, what are the position, speed, velocity and accelerations of the beetle at the following scenario? the " -0.52 m Position (m 7.5 12.5 176 time ( s)Physics Lab (Online Simulation] radians m/s, a. 6 = degrees, 6 = b- Vbeetle = _ I'll/S, beeetle = _ Procedure 11: Angular Kinematics: 1. Click \"Reset All\" and check the position of the ladybug on the turntable. Under the \"Show graphs\" select 9,0),oc graph and set the angular acceleration in such a way that the turntable moves counterclockwise. What are the directions of velocity and accelerations after the turntable rotates 1800 a) P b) f c) Vybeetle = _ 1'1'1/ 5, abeetle = _m/5 2 l/ \"/l 2. Click \"Reset All\" again and this time drag the Beetle on the turntable and put it at (3,0). Set the angular velocity to 0 rad/s and angular acceleration to 2 rad/$2. Now click \"Go\" and stop it after the turntable rotates for 10 seconds. Make sure you use different options of the graphs under the \"Show graphs\" options to answer your question below a. What are the values you read at the 5th second? Ladybug: 6 = rad, Beetle: 6 = rad, V: v 2 m/s, m/s, 3 Z a = m/s2 2 m/s b. Calculate the following velocity and accelerations at the 5th second atan : Ladybug: van = Beetle: van = m/s, m/s, atan = m/s2 m/s c. Calculate the total acceleration and compare it with the values you found in a 2 m/s Beetle: a = Ladybug: a = m/s2 3. Answer the following questions based on the graphical information below. You can try to check it with running a simulation NW (\"9"\") 19\"\" ammmazauoo degrees Ohm-t"! degrees a_ ll} a J {L b. l l -1.ouu H 0 2.5 5 7.5 10 12.5 1! c time (s) .2 , D g 5\" mum-30.00 groom 30.00 groom 3 d. g u i > 5 ~60 5 . . D 2.5 5 7.5 12.5 15 e. 5 cum-1m donnesls'2 I'VE-2. honour!" f. O a g. D 2.5 5 7.5 10 12.5 15 lime (s) Allmlll Ace-clam (Mull What is the angular acceleration? What is the angular velocity at t=0? What is the angular displacement of of the platform at 5 seconds? Where was the initial location of the ladybug? (as measured from the center of axis of rotation) What is the tangential velocity at t= 5 5? What is the tangential acceleration at t = 5 5 What is the total acceleration at t = 5 s Physics Lab (Online Simulation) MI 0.\" his\"! \"dentin (ml?!) D II 2.5 5 75 10 12.5 15 time (s) 4. Apply the following settings for the simulation and draw the graph you obtained in the space provided. a. Click \"Reset All\" and put the beetle at (2.5, 0) position b. Set the angular velocity to 20 rad/s c. Set the angular acceleration to 1 rad/s2 d. Run the simulation for 10 seconds 1mm- 7., 5 ll '3 |. 8 E '5 5 u a E 5 3 .1nnn- i .5 ' o 2.5 5 7.5 10 12.5 E 0 25 5 715 10 12.5 time (s) time (5) E 511- F 1- 3 z E " o a .. g i 3 i\" ' n 25 5 75 11: 12.5 i o 2.5 5 75 10 12.5 time (5) time(s) Follow-up Concept Questions: 1. Describe the directions of tangential velocity and accelerations for the following scenario. Support your answer with simple sketch a. A bug on a platform spinning counterclockwise with constant speed b. A bug on a platform spinning clockwise with constant speed Physics Lab (Online Simulation] c. A ladybug is clinging to the rim of a wheel, which is spinning counterclockwise and is speeding up 2. Set the angle and the angular acceleration to zero. Set the angular velocity to 2.0 rad/s. Predict how far the ladybug will rotate in radians after 5.0 5. Check your prediction with the simulation. Was it correct? 3. Set the angle to 5.0 rad and the angular acceleration to zero. Set the angular velocity to 3.5 rad/s. Predict the angle at which the ladybug will be at after 4.5 5. Check your prediction with the simulation. Was it correct? 4. Set the angle to zero, the angular velocity to 2.0 rad/s, and the angular acceleration to be 0.30 rad/$2. Predict how fast the ladybug will rotate after 5.0 5. Check your prediction with the simulation. Was it correct