Question: 7. (bonus) Let the function f : R - R be strictly increasing and strictly convex, e.g both the first and second derivatives are positive
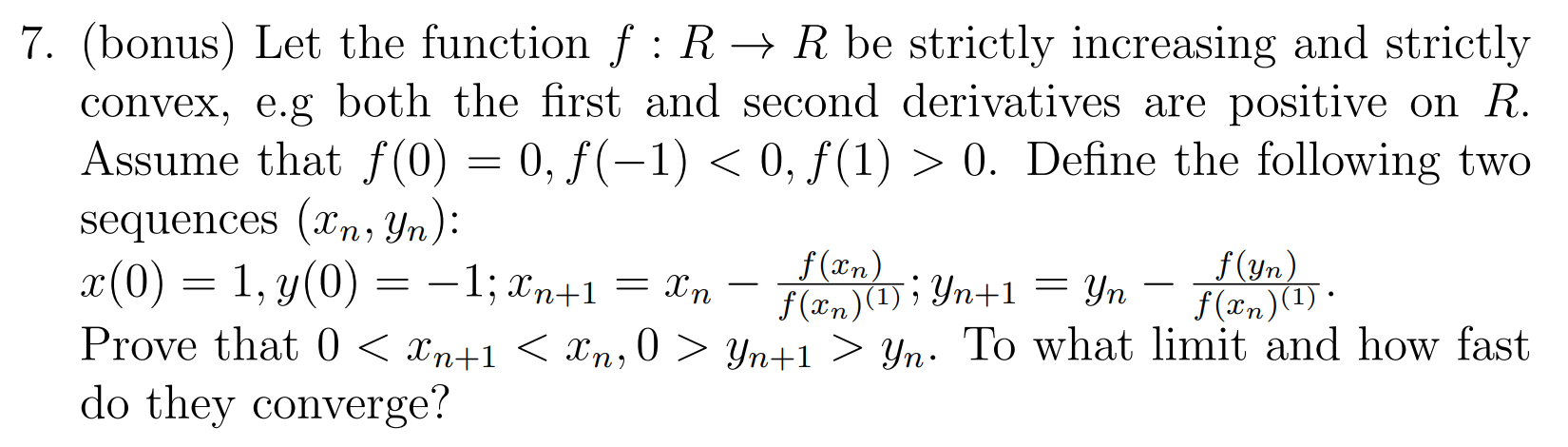

Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


