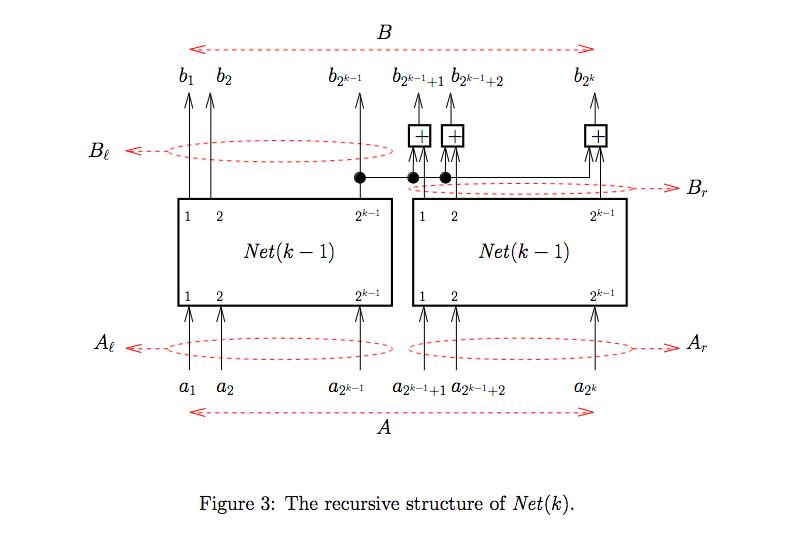
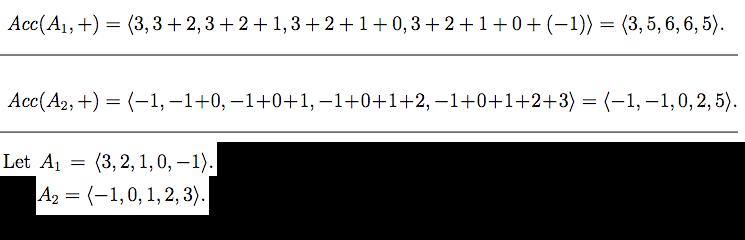
7. Consider network Net(k) defined recursively in Homework-I (see Figure 3). Prove the following for Net(k) (for k0). For this problem we will use the operation + (regular addition) on the set of integers (only for convenience the results you prove below are valid for all associative operations). Other problems in this set will use different operations. (a) Prove that for all k 0, Net(k) correctly computes Acc(A) (as defined in the first set of homework problems), for any 2-input list A. 15 points (b) Let W(k) denote the number of adders in Net(k) (for k0). Prove by induction on k 20 that W(k)= k2k-1. 15 points (c) Let T(k) denote the delay of Net(k) (for k 0); the delay is in terms of unit adder delays as in the first set of homework problems. Observe from Figure 3 of problem set 1, that in Net(k), the recursive Net (k-1) blocks operate concurrently. Thus their collective delay is the larger of the times taken by each of them (rather than the sum of their delays). The last bank of adders outside the Net(k-1)'s, on the other hand, have to wait for the recursive blocks to finish. Determine a recurrence relation for T(k). Make a guess for a closed form expres- sion for T(k) and prove your guess correct by induction on k 0. 30 points Be Ae b b ^ 1 1 2 a1 a2 B b2k-1 b2k-1+1bk-1+2 Net (k-1) 24-1 2-1 1 2 A 1 2 Net (k-1) a2k-1 a2k-1+1 a2k-1+2 bak 2k-1 Figure 3: The recursive structure of Net(k). 2-1 a2k Br Ar Acc(A, +) (3, 3+2, 3+2+1, 3+2+1+0,3+2+1+0+ (-1)) = (3, 5, 6, 6,5). = Acc(A, +) = (-1,-1+0, 1+0+1, 1+0+1+2,1+0+1+2+3)= (-1,-1, 0, 2, 5). Let A (3, 2, 1, 0, -1). = A = (-1,0, 1, 2, 3).