Question: 7) (i) If k is a positive integer, A is an eigenvalue of a matrix A, and v is a corresponding eigenvector, then A

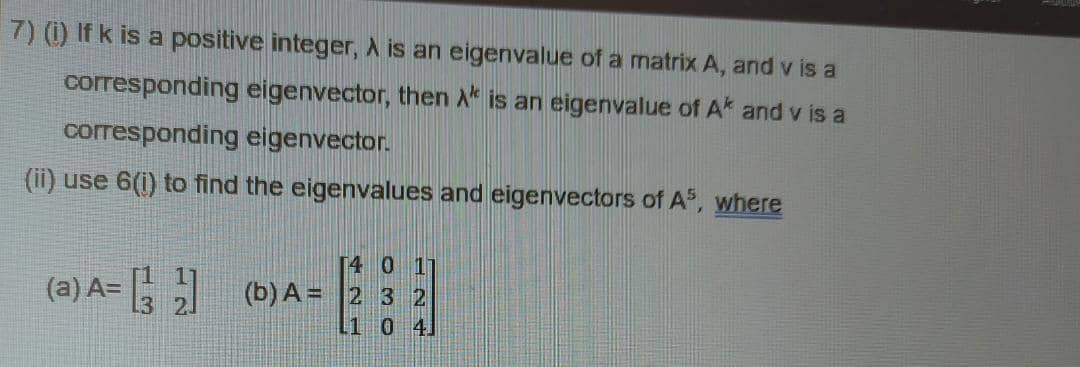
7) (i) If k is a positive integer, A is an eigenvalue

7) (i) If k is a positive integer, A is an eigenvalue of a matrix A, and v is a corresponding eigenvector, then A is an eigenvalue of A* and v is a corresponding eigenvector. (ii) use 6(i) to find the eigenvalues and eigenvectors of A5, where (a) A= [32] [401 (b) A= 2 3 2 L1 0 4

Step by Step Solution

★★★★★

3.39 Rating (161 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

The eigen values of matrix A are 3 and 0 The eigenvector Corresponding to 13 is ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

The course credit hours and grades for Bills fall semester are given below. At his college, an A is worth six grade points, a B four points, a C two points, and a D one point. Solve the problems...

Decide if each vector lies in the range of the map from R3 to R2 represented with respect to the standard bases by the matrix. (a) (b) 1 1 3 1 3 6 0 4

The capital asset pricing model (CAPM) is an important model in the field of finance. It explains variations in the rate of return on a security as a function of the rate of return on a portfolio...

An auto maker is interested in information about how long transmissions last. A sample of transmissions are run constantly and the number of miles before the transmission fails is recorded. The auto...

Hello, please help me with these questions, and give explanations for the answers. Please don't use cursive as I can't read that, and please don't type the explanations. These are practice examples I...

7 4 0 :9 points) The matrix A = 8 6 3 has an eigenvalue A = 3. 3 1 3 =ind an eigenvector for this eigenvalue. Try to solve the following problem WITHOUT computing all eigenvalues. 0 0 1 _' 1 The...

Task 2 : Eigenvector Calculation Assignment: Create a C program that calculates the eigenvector corresponding to a given eigenvalue of a square matrix. The program should implement the inverse...

Please solve this 1 st year question as fast as possible (best in 1 hour), I will immediately give a helpful rating {a} (6 marks) Let A be an invertible matrix. Let A be an eigenvalue of A, with...

Let A be an n x n matrix: If v is an eigenvector of A corresponding to the eigenvalue t , find an eigenvector of A k where k is a positive integer. * t is supposed to be lambda but there is no lambda...

MAT 275 Homework 6 Please submit your work of Homework 6 on Blackboard by Thursday, December 3rd by 11:59 pm. 2 0 1 (1) Find the eigenvalues of 0 1 0. 1 0 2 (a) 1, 2. (b) 1, 3. (c) 0, 3, 1. (d) 0, 2,...

4. An industrial strength drain cleaner contains 9 kg of H2O and 5 kg of NaOH. What are the mole fractions of each component in the solution? 5. A saturated salicylic acid in methanol contains 64 kg...

Company has one factory making "whizzo's" which they sell to the general public. Company bought the factory 5 years ago paying $40 million. . The FMV (fair market value) of the factory is now $55...

Question 2 The commencement of the Malaysian Private Entities Reporting Standard ( MPERS ) in January 2 0 1 6 is both timely and essential. MPERS highlights the growing importance of local private...

(d) 2 sin A tan A =? la+cos A) (1-cos A)J (a) 2 sin A (b) 2 tan A sec A (c) 2 sec A (d) 2 cosec A tan A tan A

DC-116 Eagle's Progressive Applied M- Example 18. If y log (x + Va? + x ), prove that (a + x)y2 + xy, = 0

robability that it is either a spa 1 -) Evaluate - dx 1+ sin x tan x sec? x dx 1- tan2 x Evaluate Find two numbers whose su Ify= (x+sinx) (x- co

X+y=34 X-y'%3544 ecO x y de z23es Dab? 2) 4, 3 *) t 5, 3

m If sinx=- 1+m then find 'tan x'. A) 1+m C)

The return of goods to the supplier will affect the purchase account. Question 27Answer True False

If 4x - 9 f(x) x2 - 4X + 7 for x 0, find f(x). lim

Find the sum of the series. a. b. c. 3) 2 [tan-l(n + 1)-tan-in] 2! 3! 4!

Use the Alternating Series Estimation Theorem or Taylor's Inequality to estimate the range of values of for which the given approximation is accurate to within the stated error. Check your answer...

MY Auto body's adjusted trial balance on December 31, 2014, appears in the work sheet as follows: Required 1. Prepare closing entries. 2. Prepare the post-closing trial balance at December 31, 2014.

The following closing entries were prepared for Apex Architectural Designs regarding its year just ended June 30, 2014: Required 1. Prepare an income statement based on the information provided. 2....

The unadjusted trial balance for Lewis Fitness Centre as of December 31, 2014, follows: Information necessary to prepare adjusting entries is as follows: a. As of December 31, employees have earned...