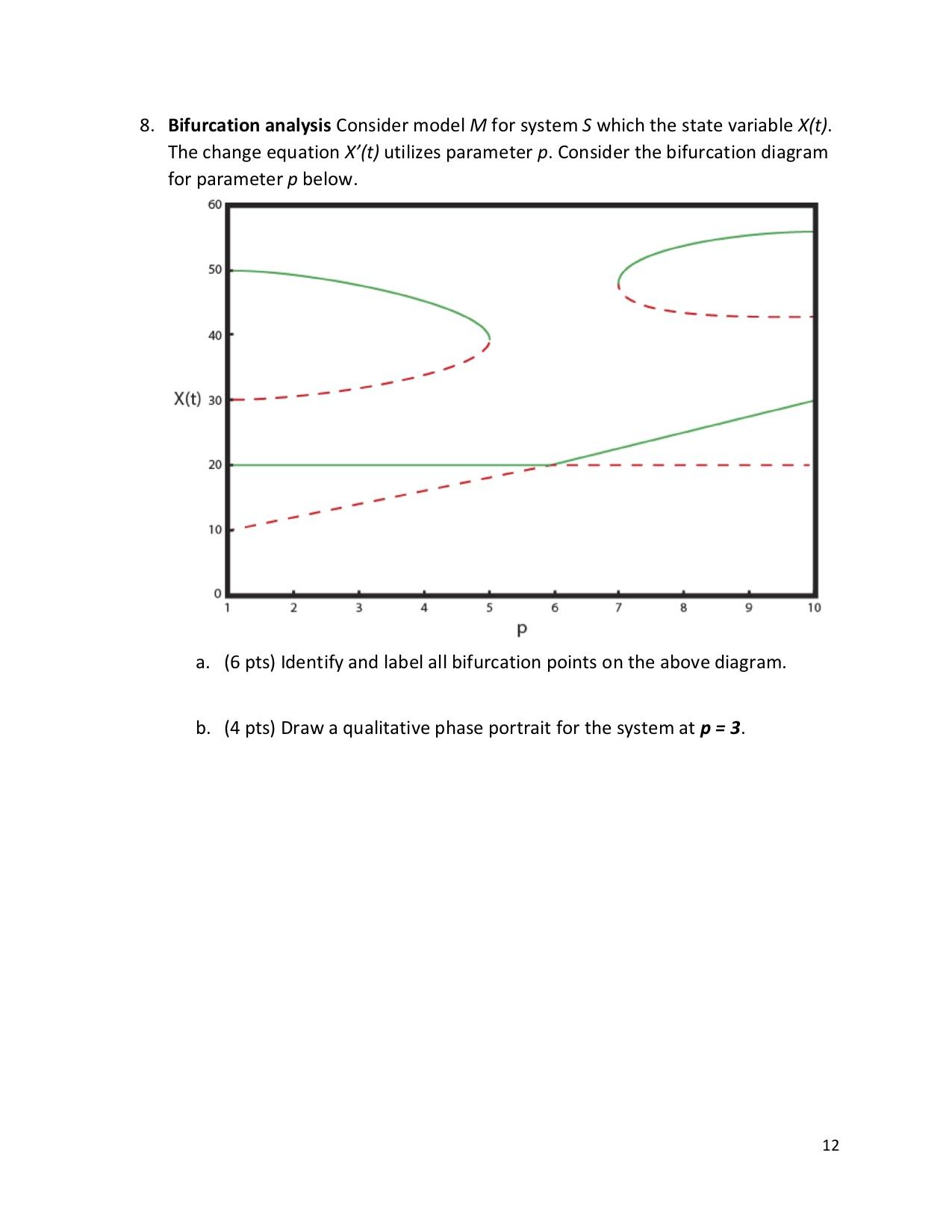
7. Light and shadow continue their eternal dance. Shadow grows in the spaces that light has left while the inhabitants of this universe are wont to produce light where the shadow is darkest. L' = S S' = -L (8 pts) Sketch the vector field of this system using a minimum of eight vectors. Then sketch out two approximate trajectories for this system and name the 2D equilibrium point that is present. S -3 -2 0 3 sink center stable spiral saddle point 11 8. Bifurcation analysis Consider model M for system S which the state variable X(t). The change equation X'(t) utilizes parameter p. Consider the bifurcation diagram for parameter p below. 60 50 40 X(t) 30 20 10 0 1 2 3 5 P 7 8 9 10 a. (6 pts) Identify and label all bifurcation points on the above diagram. b. (4 pts) Draw a qualitative phase portrait for the system at p = 3. 12 9. You are provided the following code, which analyzes a population model. def test(Nprime, eqlist): dNprimedN(N)=diff(Nprime(N)) for eqpoint in eqlist: if dNprimedN(eqpoint)>0: print("1st kind of EP") elif dNprimedN(eqlist)