Question: 8. [0/8 Points] DETAILS PREVIOUS ANSWERS This exercise analyzes the function f(x) whose derivative f'(x) is graphed below. The domain of this function is the
![8. [0/8 Points] DETAILS PREVIOUS ANSWERS This exercise analyzes the function](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6661271848eae_03266612718124cb.jpg)
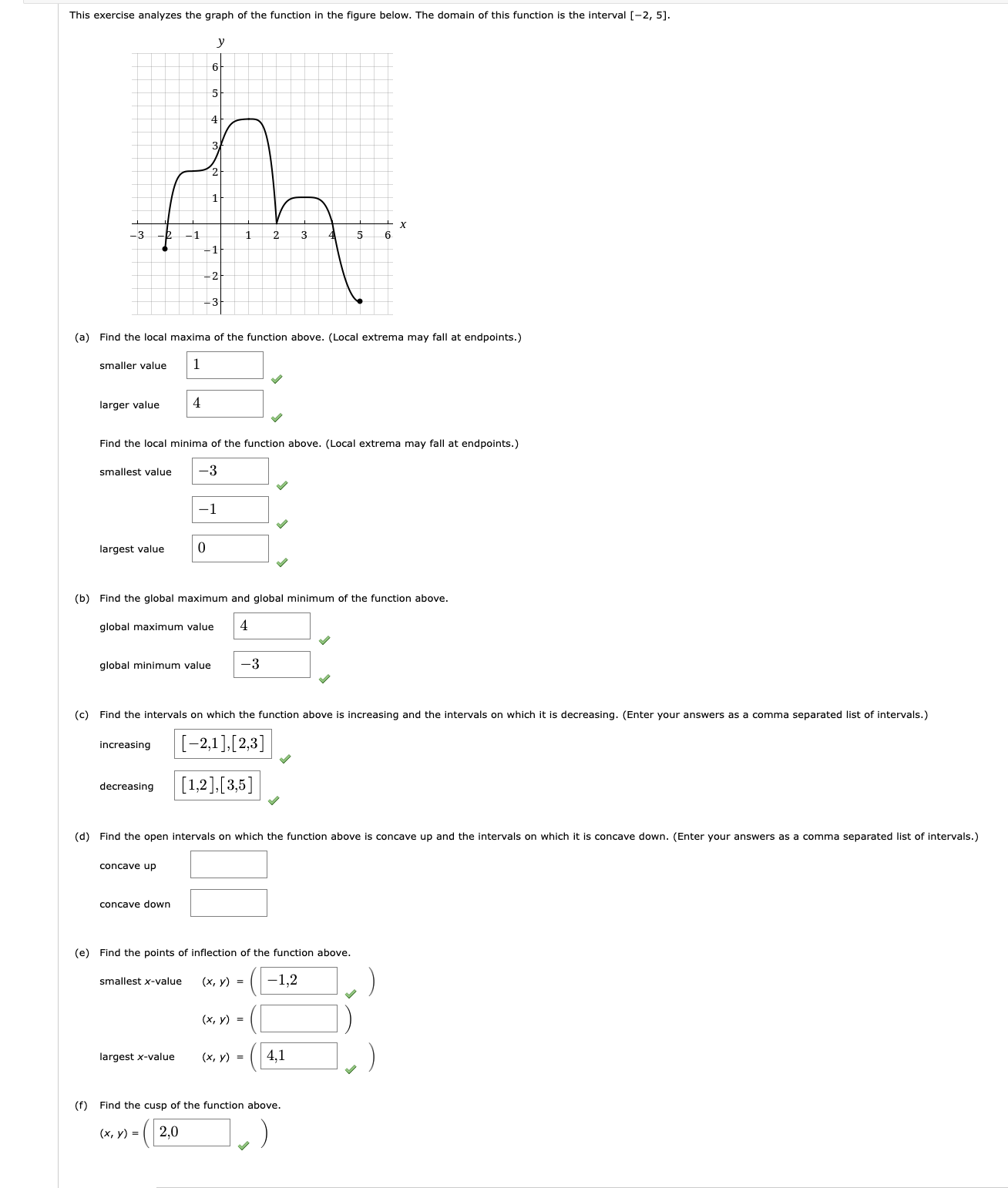
![is the interval [-3, 4]. f (x) -4 -2 - - 21](https://s3.amazonaws.com/si.experts.images/answers/2024/06/66612718ee1a4_03266612718d241c.jpg)

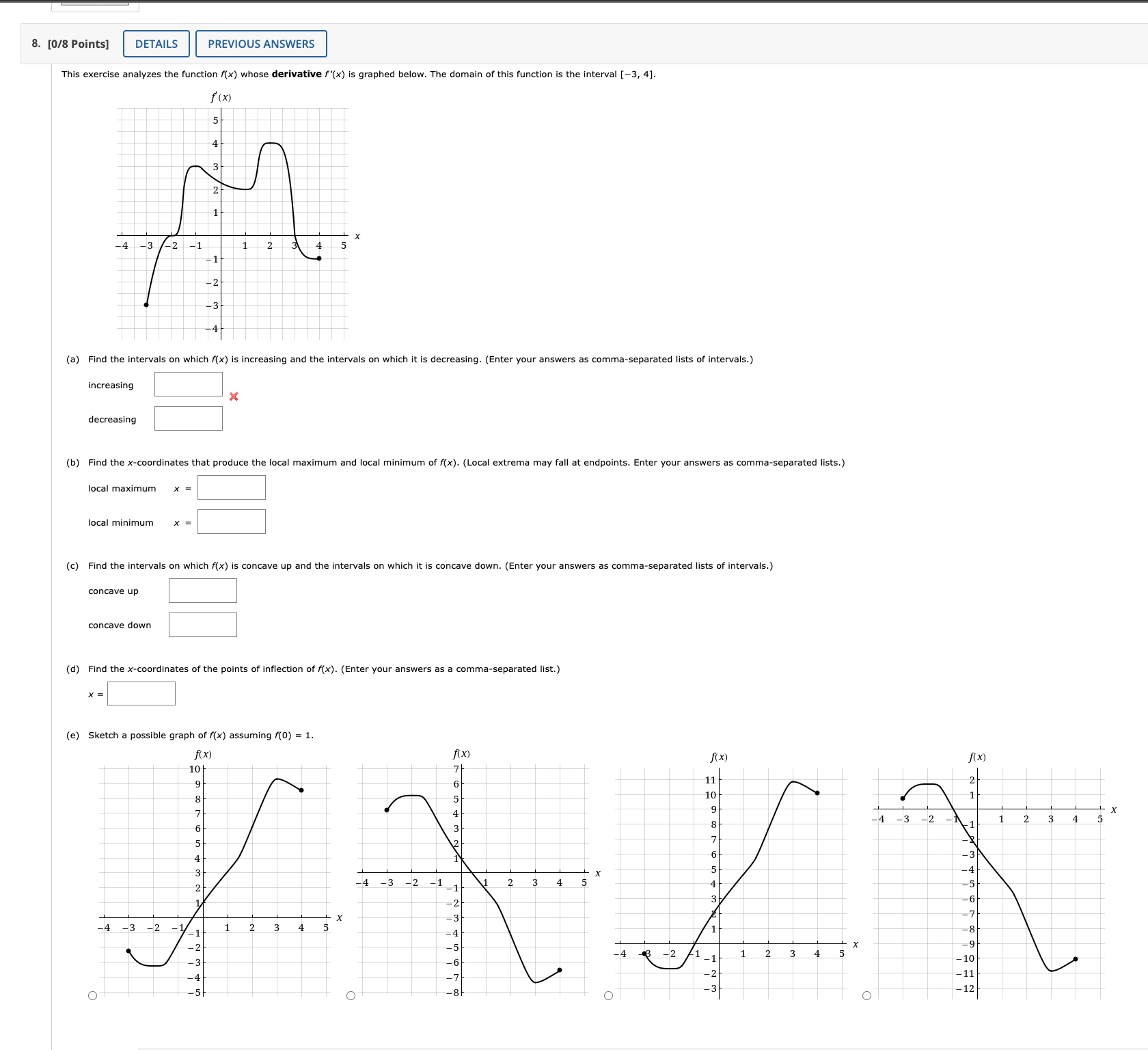
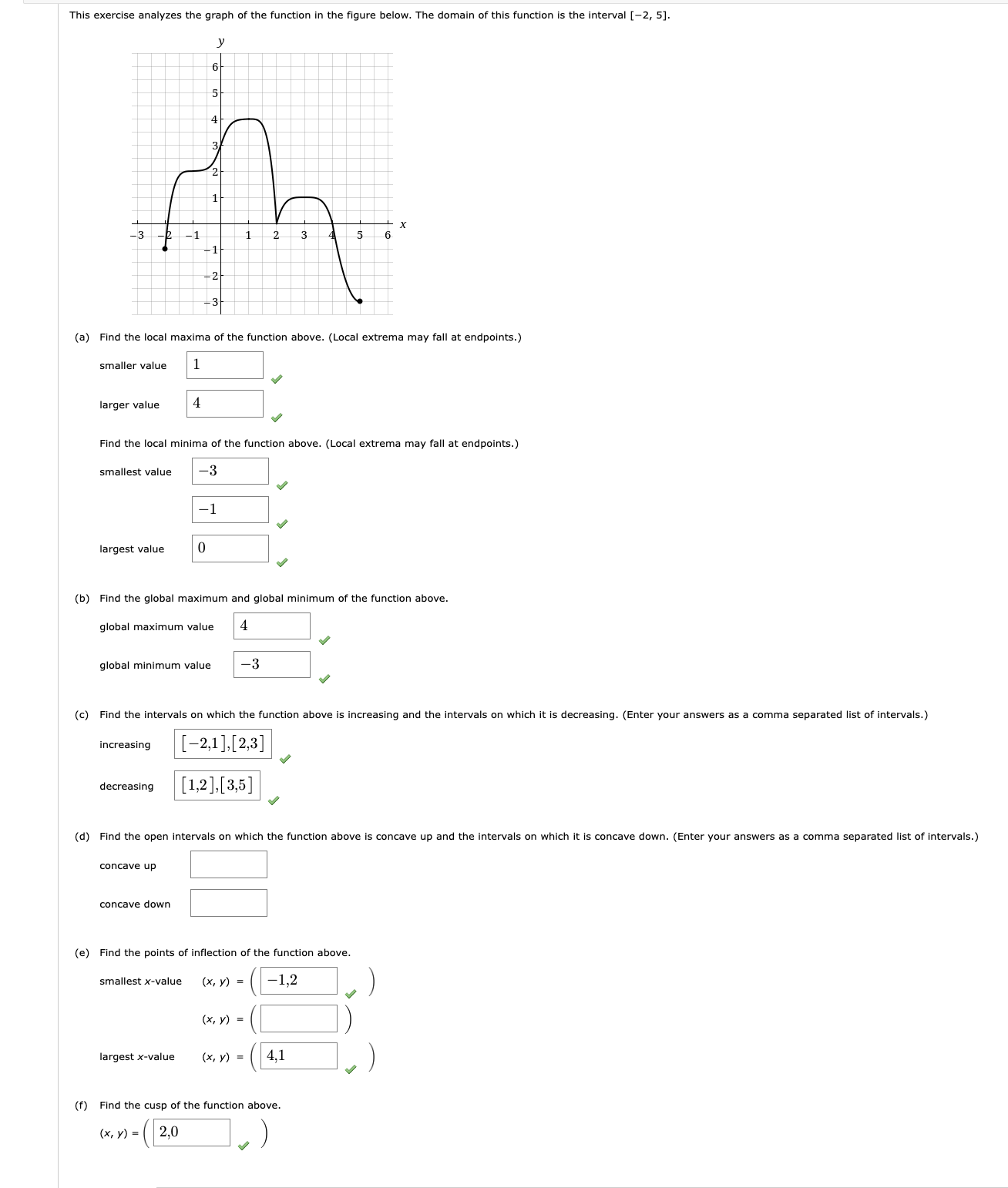
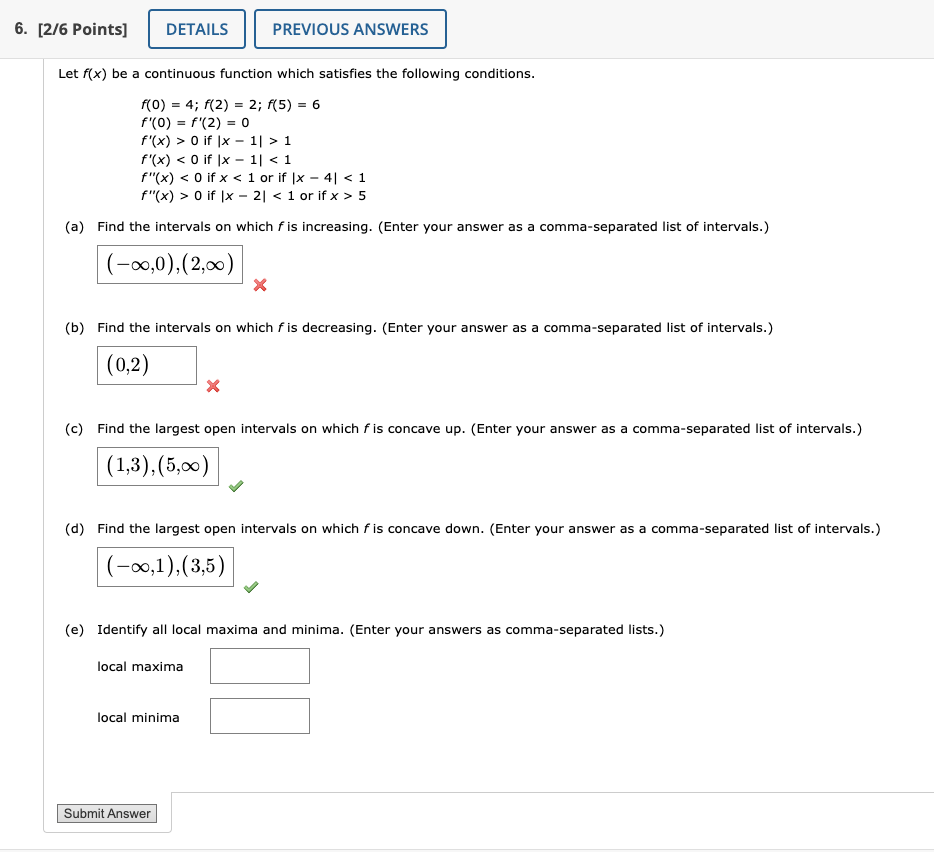

8. [0/8 Points] DETAILS PREVIOUS ANSWERS This exercise analyzes the function f(x) whose derivative f'(x) is graphed below. The domain of this function is the interval [-3, 4]. f (x) -4 -2 - - 21 - 3 (a) Find the intervals on which f(x) is increasing and the intervals on which it is decreasing. (Enter your answers as comma-separated lists of intervals.) increasing decreasing (b) Find the x-coordinates that produce the local maximum and local minimum of f(x). (Local extrema may fall at endpoints. Enter your answers as comma-separated lists.) local maximum * = local minimum (c) Find the intervals on which f(x) is concave up and the intervals on which it is concave down. (Enter your answers as comma-separated lists of intervals.) concave up concave down (d) Find the x-coordinates of the points of inflection of f(x). (Enter your answers as a comma-separated list.) (e) Sketch a possible graph of f(x) assuming f(0) = 1. O OThis exercise analyzes the graph of the function in me figure below. The domain of this function is the interval [2, 5]. (a) Find the local maxima of the function above. (Local extrema may fall at endpoints.) smaller value 1 J larger value 4 J Find the local minima of the Function above. (Local extrema may fall at endpoints.) smallest value 3 J 1 J largest value 0 J (b) Find the global maximum and global minimum of the function above. global maximum value 4 J global minimum value 3 J (c) Find the intervals on which the function above is increasing and the intervals on which it is decreasing. (Enter your answers as a comma separated list of intervals.) increasing [2,1],:2,3] decreasing [1.2],[3,5] J (d) Find the open intervals on which line function above is concave up and the intervals on which it is concave down. (Enter your answers as a comma separated list of intervals.) concave up concave down (e) Find the points of inection of the function above. smallest x-value (x, y} = ( 1.2 ) J (x. V) = ( ) largestx-value (x, y) : ( 4:1 ) J (f) Find the cusp of the function above. (x. y) :( 2:0 ) J 6. [2/6 Points] DETAILS PREVIOUS ANSWERS Let f(x) be a continuous function which satisfies the following conditions. f(0) = 4; f(2) = 2; f(5) = 6 f'(0) = f'(2) = 0 f'(x) > 0 if |x - 1| > 1 f'(x) 0 if |x - 2| 5 (a) Find the intervals on which f is increasing. (Enter your answer as a comma-separated list of intervals.) (-00,0), (2,00) X (b) Find the intervals on which f is decreasing. (Enter your answer as a comma-separated list of intervals.) (0,2) X (c) Find the largest open intervals on which fis concave up. (Enter your answer as a comma-separated list of intervals.) (1,3), (5,00) (d) Find the largest open intervals on which fis concave down. (Enter your answer as a comma-separated list of intervals.) (-00,1), (3,5) (e) Identify all local maxima and minima. (Enter your answers as comma-separated lists.) local maxima al minima Submit AnswerConsider the function f(x ) = _ (a) Find the domain of f. (Enter your answer using interval notation.) (-00 , - 2 ) U ( - 2, 2 ) U ( 2,00 ) (b) Find the intervals on which f is increasing. (Enter your answer as a comma-separated list of intervals.) (-00, - 2), (-2,0) Find the intervals on which fis decreasing. (Enter your answer as a comma-separated list of intervals.) (0,2), (2,00) (c) Find the open intervals on which fis concave up. (Enter your answer as a comma-separated list of intervals.) (-00, - 2), (2,00) Find the open intervals on which f is concave down. (Enter your answer as a comma-separated list of intervals.) (-2,2) (d) Find the vertical asymptotes of f. smaller x-value x = -2 larger x-value x = 2 Find the left- and right-handed limits as we approach a vertical asymptote. As we approach the smaller x-value, the left-handed limit of fis co . and the right-handed limit is -co . . As we approach the larger x-value, the left-handed limit of fis -0| and the right-handed limit is o . (e) Find the horizontal asymptotes of f. (Enter your answers as a comma-separated list of equations.) (f) Find the x-intercept. x = 0 Find the y-intercept. y = 0 (9) Use the information obtained to sketch the graph of the function. 10 10 10 5 10 -10
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


