Question: 8. Let F be an arbitrary field. Let Ap(x) be the companion matrix of a prime polynomial p(x) e F[x]. Prove that D(XI - Ap(x))
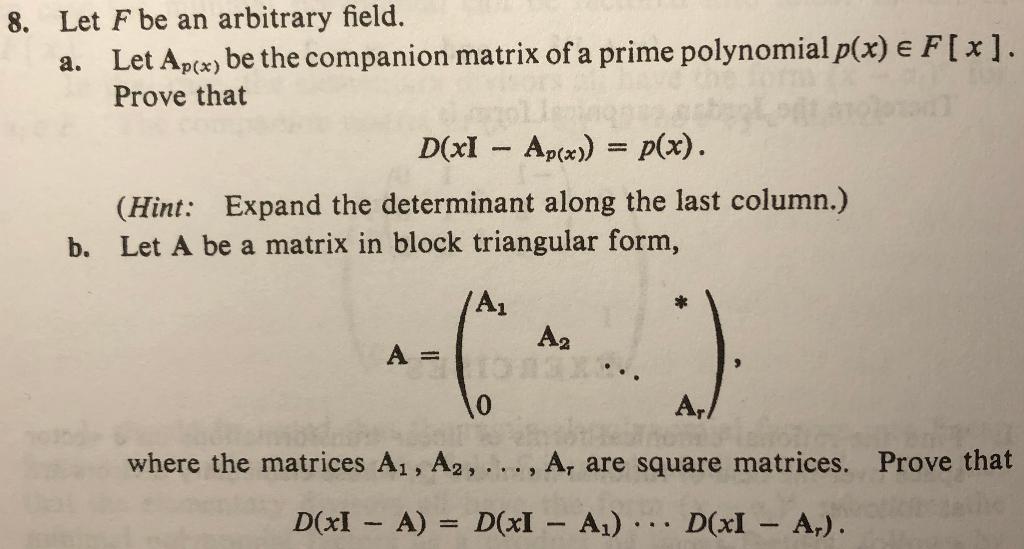
![companion matrix of a prime polynomial p(x) e F[x]. Prove that D(XI](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2024/09/66e866403dea3_55966e8663fbee84.jpg)
8. Let F be an arbitrary field. Let Ap(x) be the companion matrix of a prime polynomial p(x) e F[x]. Prove that D(XI - Ap(x)) = p(x). (Hint: Expand the determinant along the last column.) b. Let A be a matrix in block triangular form, A1 A2 A = ) 10 Ar! whe the matrices A1, A2, ..., A, are square matrices. Prove that D(XI - A) = D(xI - A)... D(XI - Ar). c. Let A be the companion matrix of a prime power p(x) F[x]. Prove that D(xI - A) = P(x) d. Let A be a matrix whose elementary divisors are {p1(x)ei, ...,Pr(x);}. Prove that D(xI - A) = P1(x)ei ... p.(x). e. Prove the Cayley-Hamilton theorem for matrices with coefficients in F: If h(x) D(x1 - A), then h(A) = 0. 8. Let F be an arbitrary field. Let Ap(x) be the companion matrix of a prime polynomial p(x) e F[x]. Prove that D(XI - Ap(x)) = p(x). (Hint: Expand the determinant along the last column.) b. Let A be a matrix in block triangular form, A1 A2 A = ) 10 Ar! whe the matrices A1, A2, ..., A, are square matrices. Prove that D(XI - A) = D(xI - A)... D(XI - Ar). c. Let A be the companion matrix of a prime power p(x) F[x]. Prove that D(xI - A) = P(x) d. Let A be a matrix whose elementary divisors are {p1(x)ei, ...,Pr(x);}. Prove that D(xI - A) = P1(x)ei ... p.(x). e. Prove the Cayley-Hamilton theorem for matrices with coefficients in F: If h(x) D(x1 - A), then h(A) = 0
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


