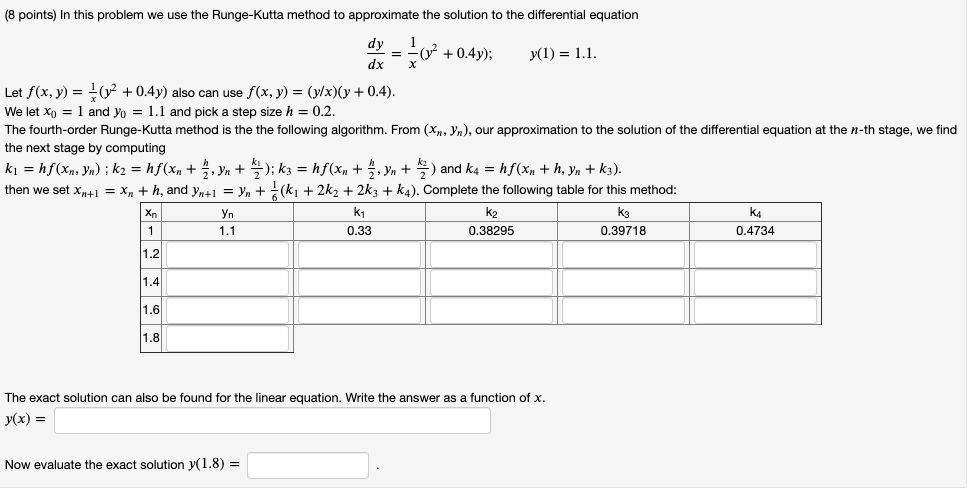
(8 points) In this problem we use the Runge-Kutta method to approximate the solution to the differential equation -(y + 0.4y); y(1) = 1.1. Let f(x, y) = (y2 + 0.4y) also can use f(x, y) = (y/x)(y + 0.4). We let Xo = 1 and yo = 1.1 and pick a step size h = 0.2. The fourth-order Runge-Kutta method is the the following algorithm. From (Xn, yn), our approximation to the solution of the differential equation at the n-th stage, we find the next stage by computing k = hf(xn, yn); k2 = hf(xn +, Y + "); k3 = hf(xn+ , Yn + 2) and k4 = hf(x, + h, yn + kg). then we set Xn+1 = x, + h, and Yn+1 = y + (ki + 2k2 + 2k3 + ka). Complete the following table for this method: yn k, k2 1.1 0.33 0.38295 0.39718 0.4734 k3 KA The exact solution can also be found for the linear equation. Write the answer as a function of x. y(x) = Now evaluate the exact solution y(1.8) =