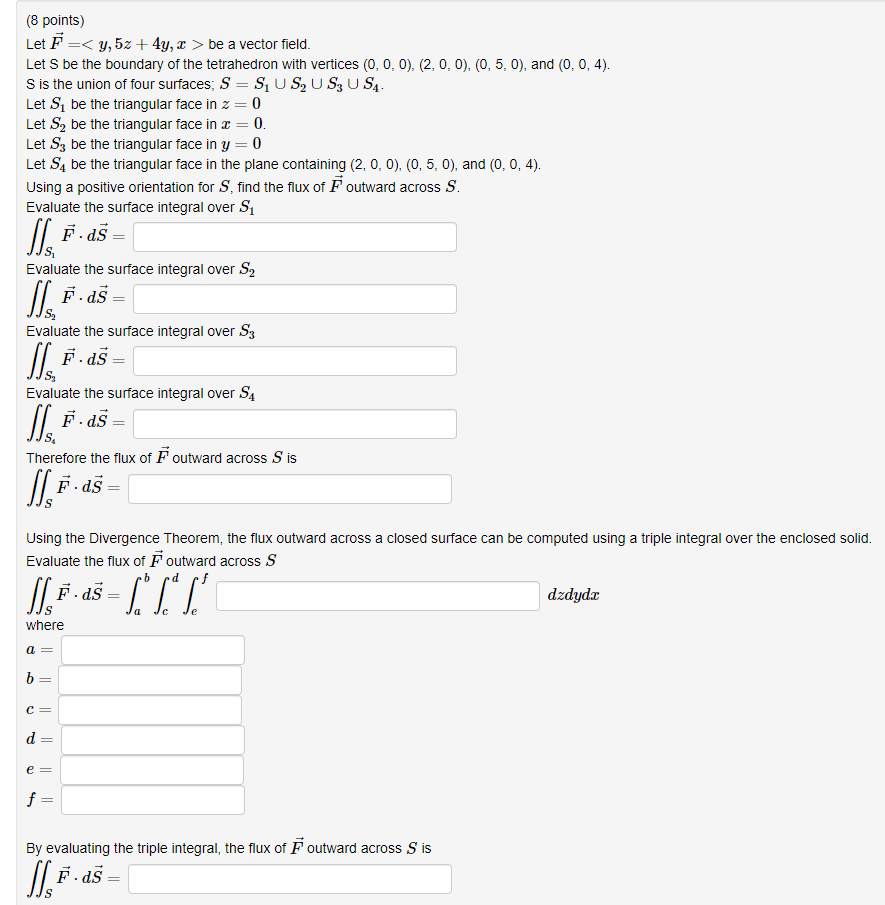
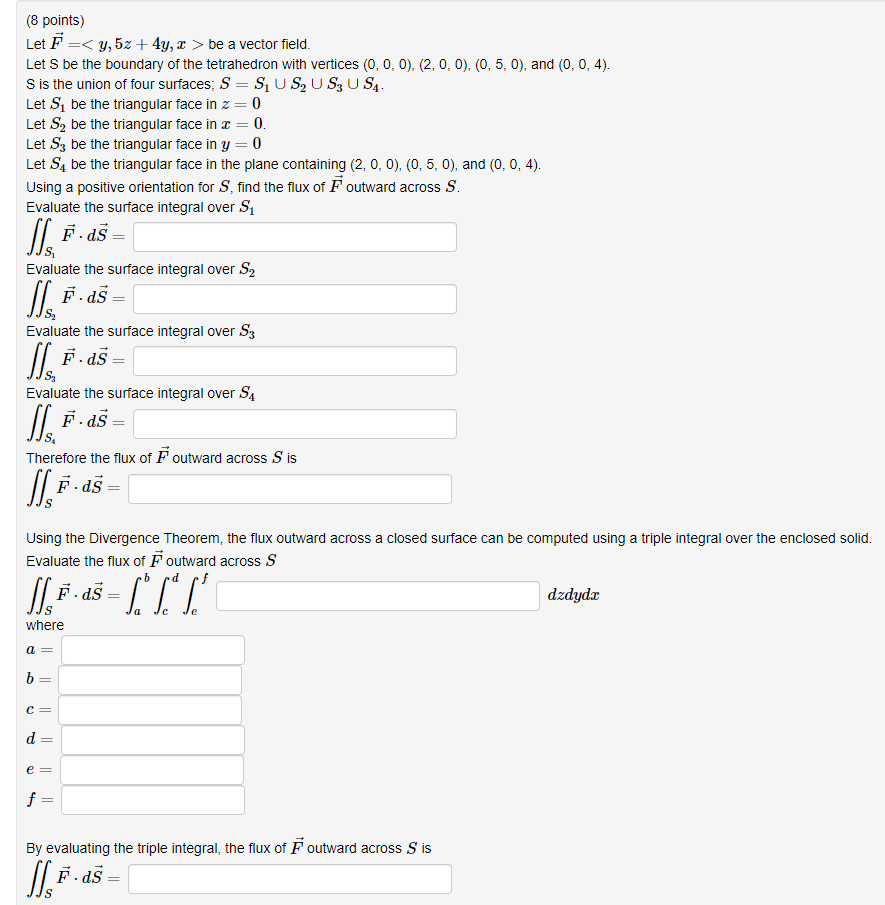
(8 points) Let F = > be a vector field. Let S be the boundary of the tetrahedron with vertices (0, 0, 0), (2, 0, 0), (0, 5, 0), and (0, 0, 4). S is the union of four surfaces; S = S, U S, U S; U S4. Let S1 be the triangular face in z = 0 Let S2 be the triangular face in c = 0. Let Sy be the triangular face in y = 0 Let S4 be the triangular face in the plane containing (2, 0, 0), (0, 5, 0), and (0, 0, 4). Using a positive orientation for S, find the flux of F outward across S. Evaluate the surface integral over S, I F .as - Evaluate the surface integral over S2 Evaluate the surface integral over S3 Evaluate the surface integral over S4 If F .as - Therefore the flux of F outward across S is F . as = Using the Divergence Theorem, the flux outward across a closed surface can be computed using a triple integral over the enclosed solid. Evaluate the flux of F outward across S dadydx where a= b = C = d. = e = f = By evaluating the triple integral, the flux of F outward across S is 1, F . as =