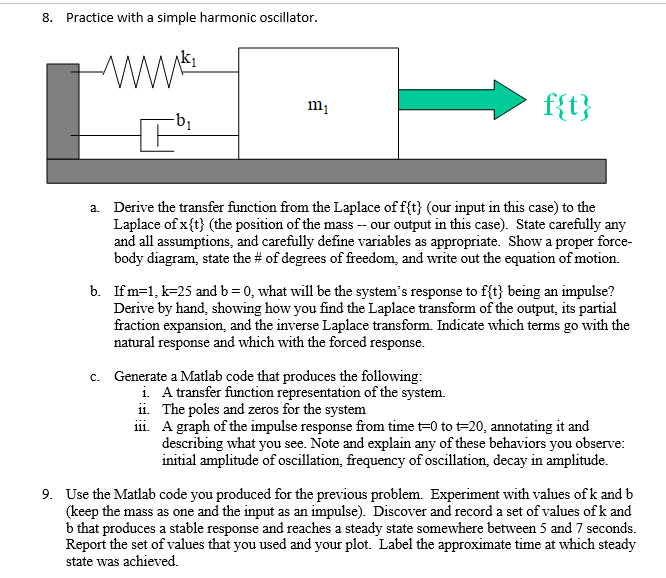
8. Practice with a simple harmonic oscillator. www m -b f{t} a. Derive the transfer function from the Laplace of f{t} (our input in this case) to the Laplace of x{t} (the position of the mass -- our output in this case). State carefully any and all assumptions, and carefully define variables as appropriate. Show a proper force- body diagram, state the # of degrees of freedom, and write out the equation of motion. b. If m=1, k=25 and b = 0, what will be the system's response to f{t} being an impulse? Derive by hand, showing how you find the Laplace transform of the output, its partial fraction expansion, and the inverse Laplace transform. Indicate which terms go with the natural response and which with the forced response. c. Generate a Matlab code that produces the following: i. A transfer function representation of the system. ii. The poles and zeros for the system iii. A graph of the impulse response from time t=0 to t=20, annotating it and describing what you see. Note and explain any of these behaviors you observe: initial amplitude of oscillation, frequency of oscillation, decay in amplitude. 9. Use the Matlab code you produced for the previous problem. Experiment with values of k and b (keep the mass as one and the input as an impulse). Discover and record a set of values of k and b that produces a stable response and reaches a steady state somewhere between 5 and 7 seconds. Report the set of values that you used and your plot. Label the approximate time at which steady state was achieved.