Question: 8) y = e*, y2 2x = e are all solutions to y (4 (4) - - 4y''' + 3y + 4y' 4y =

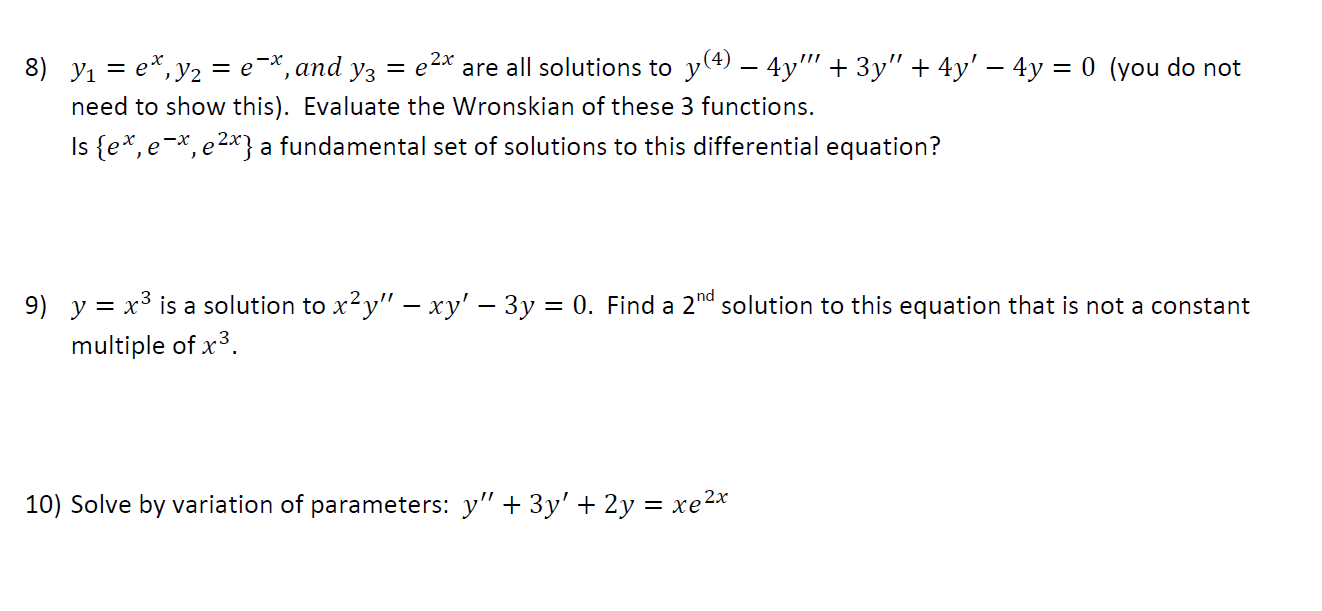
8) y = e*, y2 2x = e are all solutions to y (4 (4) - - 4y''' + 3y + 4y' 4y = 0 (you do not e-x, and y3 need to show this). Evaluate the Wronskian of these 3 functions. Is {ex, ex, ex} a fundamental set of solutions to this differential equation? 9) y = x is a solution to xy" - xy' - 3y = 0. Find a 2nd solution to this equation that is not a constant multiple of x3. 10) Solve by variation of parameters: y" + 3y' + 2y = xex

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

One of the great dangers in allocating common costs is that such allocations can make a product line look less profitable than it really is. (Enter only one word per blank.)

CANMNMM January of this year. (a) Each item will be held in a record. Describe all the data structures that must refer to these records to implement the required functionality. Describe all the...

Portray in words what transforms you would have to make to your execution to some degree (a) to accomplish this and remark on the benefits and detriments of this thought.You are approached to compose...

Use a calculator to evaluate an ordinary annuity formula \[A=m\left[\frac{\left(1+\frac{r}{n}ight)^{n t}-1}{\frac{r}{n}}ight]\] for $m, r$, and $t$ (respectively) given in Problems 7-22. Assume...

At = 0.05, can you support the claim that the proportion of men ages 18 to 24 living in their parents homes was greater in 2012 than in 2000? Use the figure below, which shows the percentages of 18-...

What term does IFRS use for leases that result in the lessee acquiring the use and control of an asset through obtaining financing from the lessor?

What are the key differences?

Kaplan Services Company (KSC) has 60 employees, 36 of whom are assigned to Division A and 24 to Division B. KSC incurred $330,000 of fringe benefits cost during 2014. Required Determine the amount of...

Johnson Company estimates that its production workers will work 88,400 direct labor hours to produce 9,170 units during the upcoming period and that overhead costs will amount to $1,091,230. During...

Use the table below to perform the tasks mentioned below: a. Conditional formatting to highlight the marks of students which are more than 75. b. Use the slicer tool to filter data based on the...

1. Let a, b R, a Answered: 1 week ago

Case 7.1 Incoterms (CIF) A contract of sale was ent between an American company, BAT Inc., of Calu- met City, Ilinois (buyer), and a German scientific equipment manufacturing firm, Tola (seller), for...

Luanne is an actuary who assesses data to take into account whether the data has been previously checked and verified. Which one of the following statements is correct? Available answer options...

1.Recommend two knowledge, skills, abilities, or other characteristics (KSAOs) to add to the dog trainer job description that align with the shelter's goals. 2.Explain how the shelter taking steps to...

Part I - Magnetic Fields 1) Background and Theory Part I: A magnetic field exerts a force that could be attractive or repulsive on another moving/stable magnet(s) depending on the polarities of both...

16) Perfect Clean, Inc. provides housekeeping services. The following financial data have been provided. Service Revenue $80,000 Cleaning Supplies Used 22,000 Wages Expense 19,350 Office Rent Expense...

In the simple quantity theory of money, what will lead to an increase in aggregate demand? In monetarism, what will lead to an increase in aggregate demand?

3 Using the data in Exercise 2, assume that the overhead for the project is given by Overhead = $2,000 + a * $1,000 per day What is the project duration that minimizes its total cost if: a. a=1? b. a...

=+c) Give a 95% confidence interval for the average February charges of cardholders who charged $2000 in January.

=+e) What reservations, if any, do you have about the confidence intervals you made in parts c and d?