9 Consider a continuous-time Markov chain {X(t)} whose jump chain is the success run

chain from Problem 16. Give a condition on the holding time parameters ?(k), k =

0, 1, ... guaranteeing that {X(t)} has a stationary distribution (remember the previous

problem).

40 Consider a linear birth-death process where the individual birth rate is ? = 1, the

individual death rate is = 3 and there is constant immigration into the population

according to a Poisson process with rate ?. (a) State the rate diagram and the generator.

(b) Suppose that there are currently 10 individuals in the population. What is the

probability that the population size increases to 11 before it decreases to 9? (c) Suppose

that ? = 1 and that the population just became extinct. What is the expected time until

it becomes extinct again?

41 In the previous problem suppose that an immigrating individual joins the population only

if it is extinct, and otherwise leaves. Find the rate diagram, generator, and stationary

distribution.

42 Consider state 0 in a birth-death process with stationary distribution ?. Under stationary

conditions we ought to have the balance equation ?0?0 = ?11 ("rate in equals rate

out"), which is also precisely the first equation of ? G = 0. (a) Suggest how to formulate

balance equations for any three states k ?1, k, and k + 1, and show that these equations

are the same as ?G = 0. (b) Describe how the equation?G = 0 has an interpretation as

balance equations for any continuous-time Markov chain, not just birth-death processes.

43 Consider an M/M/1/r queue in equilibrium where r = 5 and the service rate equals

the arrival rate. (a) What is the proportion of lost customers? (b) How does this change

if the service rate is doubled?

44 Consider a queueing system where there is one server and no room to wait in line (i.e.,

an M/M/1/1 queue). Further suppose that the arrival rate ? and the service rate are

equal. Under stationary conditions, find the proportion of customers that are lost (a) in

this system, (b) if the service rate is doubled, (c) if one customer can wait in line, (d) if

a second server is added

Consider a continuous-time Markov chain where state i is absorbing. How should the

ith row of the generator G be defined?

34 Consider the ON/OFF system in Example 8.4.1. State the backward and forward equations and solve the forward equations. (Why are these easier to solve than the backward

equations?) What happens as t ? ??

35 Birds arrive at four bird feeders according to a Poisson process with rate one bird per

minute. If all feeders are occupied, an arriving bird leaves, but otherwise it occupies a

feeder and eats for a time that has an exponential distribution with mean one minute.

Consider this as a Markov chain where a "state" is the number of occupied feeders. The

rate diagram is given below. (a) Explain the rates in the diagram. (b) Find the generator

G. (c) If three feeders are occupied, what is the expected time until this changes? (d)

If all feeders are occupied, what is the probability that a bird arrives before a feeder

becomes free?

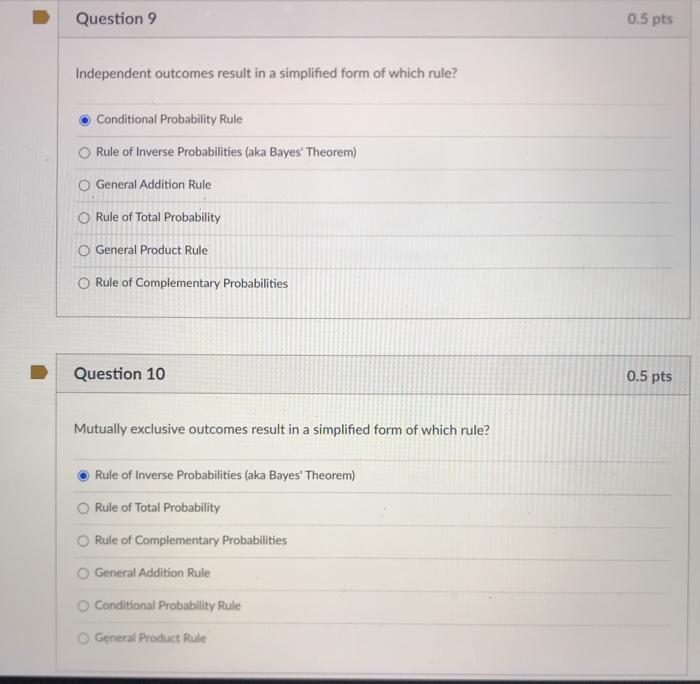
Question 9 0.5 pts Independent outcomes result in a simplified form of which rule? Conditional Probability Rule Rule of Inverse Probabilities (aka Bayes' Theorem) General Addition Rule Rule of Total Probability General Product Rule Rule of Complementary Probabilities Question 10 0.5 pts Mutually exclusive outcomes result in a simplified form of which rule? Rule of Inverse Probabilities (aka Bayes' Theorem) Rule of Total Probability O Rule of Complementary Probabilities General Addition Rule O Conditional Probability Rule O General Product Rule1. In an experiment, suppose X]. .. . . X,, |6 is i.i.d with density f(x|0) = de-28, 0 00,0 > 0. and the prior distribution of @ is Exponential distribution with density *(0) = 1 -0/8 where B is a known positive constant. (a) Find the posterior distribution of 0. (b) Find the Bayes estimator of O (the Bayes rule estimator with respect to the squared error loss). (c) Find the Bayes rule estimator of o with respect to the absolute error loss.1 Gaussian Classification Let P(x | C;) ~ N(ju;, o2) for a two-category, one-dimensional classification problem with classes C1 and C2, P(C1) = P(C2) = 1/2, and /2 > M1. (a) Find the Bayes optimal decision boundary and the corresponding Bayes decision rule. (b) The Bayes error is the probability of misclassification, Pe = P((misclassified as C1) | C2) P(C2) + P((misclassified as C2) | C1) P(C1). Show that the Bayes error associated with this decision rule is DO Pe = e -27/2 dz V2IT where a = H2 - HI 201. Suppose d1, d2, d3 and d4 are nonrandomized decision rules with risks as given in the following table: i 1 2 3 4 R(01, di) OT CO R(02, di ) 6 a) Find the minimax rule(s) amongst the nonrandomized rules D = {d1, d2, d3, d4}; b) Obtain the minimax rule in the set of randomized rules D generated by the set of rules in D. State the minimax risk of this rule. c) Find the Bayes rule and the Bayes risk for the prior (3, , ) on (01, 02). d) Express the randomized decision rule with risk point (2,5) using the given non-randomized decision rules. e) Calculate all priors for which di is a Bayes rule