9 Consider a continuous-time Markov chain {X(t)} whose jump chain is the success run

chain from Problem 16. Give a condition on the holding time parameters ?(k), k =

0, 1, ... guaranteeing that {X(t)} has a stationary distribution (remember the previous

problem).

40 Consider a linear birth-death process where the individual birth rate is ? = 1, the

individual death rate is = 3 and there is constant immigration into the population

according to a Poisson process with rate ?. (a) State the rate diagram and the generator.

(b) Suppose that there are currently 10 individuals in the population. What is the

probability that the population size increases to 11 before it decreases to 9? (c) Suppose

that ? = 1 and that the population just became extinct. What is the expected time until

it becomes extinct again?

41 In the previous problem suppose that an immigrating individual joins the population only

if it is extinct, and otherwise leaves. Find the rate diagram, generator, and stationary

distribution.

42 Consider state 0 in a birth-death process with stationary distribution ?. Under stationary

conditions we ought to have the balance equation ?0?0 = ?11 ("rate in equals rate

out"), which is also precisely the first equation of ? G = 0. (a) Suggest how to formulate

balance equations for any three states k ?1, k, and k + 1, and show that these equations

are the same as ?G = 0. (b) Describe how the equation?G = 0 has an interpretation as

balance equations for any continuous-time Markov chain, not just birth-death processes.

43 Consider an M/M/1/r queue in equilibrium where r = 5 and the service rate equals

the arrival rate. (a) What is the proportion of lost customers? (b) How does this change

if the service rate is doubled?

44 Consider a queueing system where there is one server and no room to wait in line (i.e.,

an M/M/1/1 queue). Further suppose that the arrival rate ? and the service rate are

equal. Under stationary conditions, find the proportion of customers that are lost (a) in

this system, (b) if the service rate is doubled, (c) if one customer can wait in line, (d) if

a second server is added

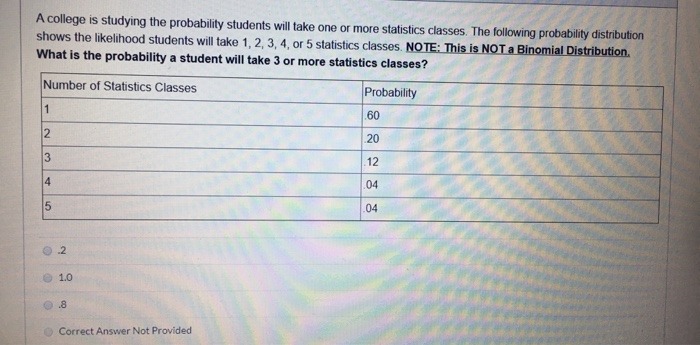
Name: 1. (15 points) Calculations under common probability distributions. Include one or two calculation steps such that you may still get the points even if the final numbers are wrong. (a) (5 points) Suppose that we have a biased coin with the probability of heads being 0.6. What is the odds ratio for heads? (b) (5 points) Suppose that the number of cars passing by an intersection is 3 every 10 minutes. What is the probability of observing no more than 2 cars in ten minutes? (c) (5 points) Suppose that the highest daily temperature in September follows a normal distribution with mean 70 and standard deviation 5. What is the 95 quantile (i.c. 95th percentile - the value with an upper-tail probability of 0.05)? 2. (15 points) (a) (10 points) Fill in the following table with type I error and type II error. Decision Do not reject Ho Reject No Ho true Ha true2. Suppose 42%% of Ph.D.s in statistics/biostatistics are earned by women and a random sample 36 statistics/biostatistics Ph.Dis is obtained. (You may want to use technology to compute some of the probabilities.) a. What's the probability none of the 36 statistics/biostatistics Ph.D.s are women? b. What's the probability at least 1 of the 36 statistics/biostatistics Ph.D.s is a woman? c. How many women do you expect in the sample of the 35 statistics/biostatistics Ph.D.s? d. What's the probability fewer than half of the 36 statistics/biostatistics Ph.D.s are women?A college is studying the probability students will take one or more statistics classes. The following probability distribution shows the likelihood students will take 1, 2, 3, 4, or 5 statistics classes. NOTE: This is NOT a Binomial Distribution, What is the probability a student will take 3 or more statistics classes? Number of Statistics Classes Probability 1 60 2 20 3 12 4 04 5 04 0 2 1.0 Correct Answer Not ProvidedThe probability that a student who studies will pass Introductory Statistics is 0.9. The probability that a students who does not study will pass introductory is 0.2. 60% of students study. 24. What is the probability that a randomly selected student will pass Introductory Statistics? 25. If a randomly selected student passes Introductory Statistics, what is the probability that the student studied