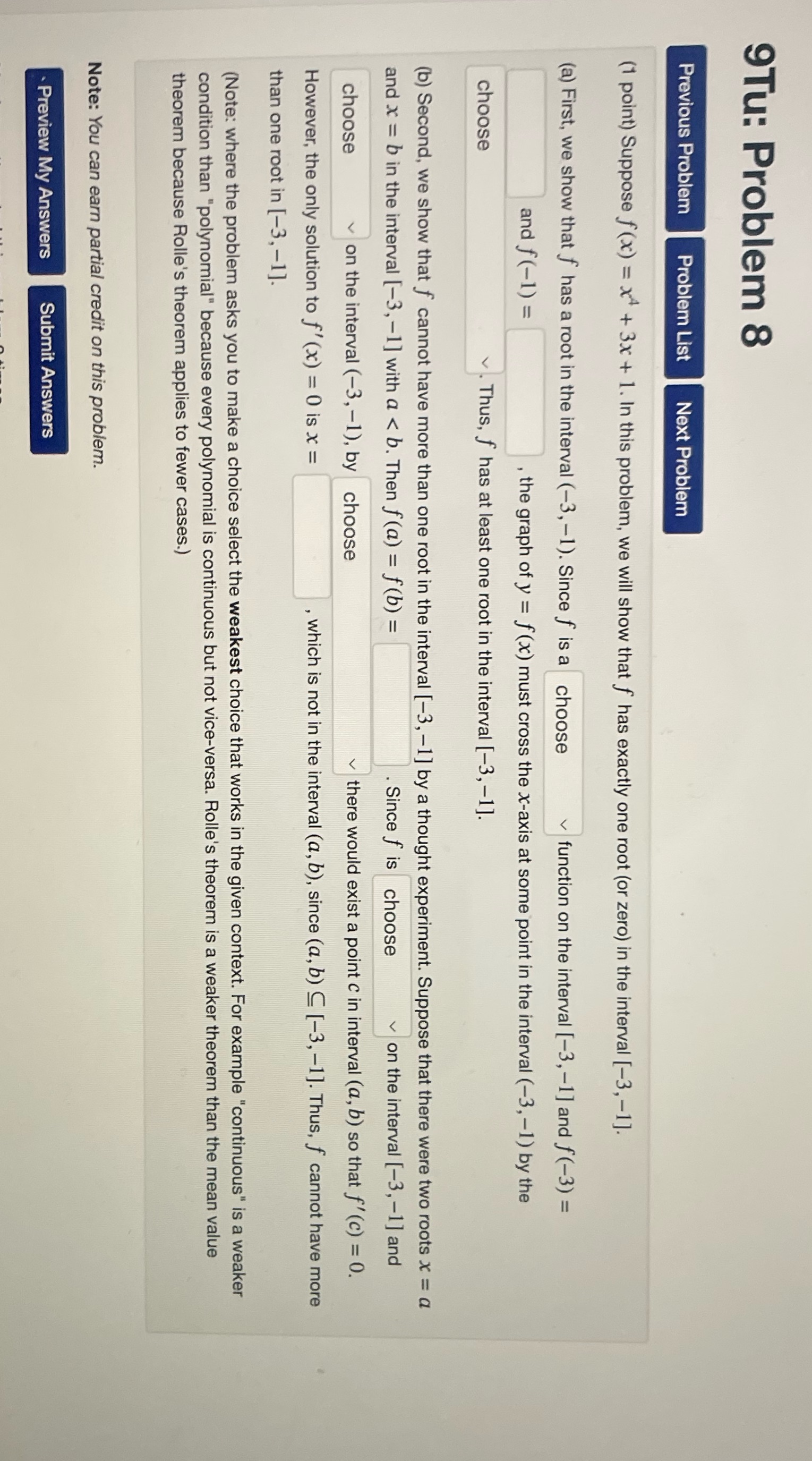
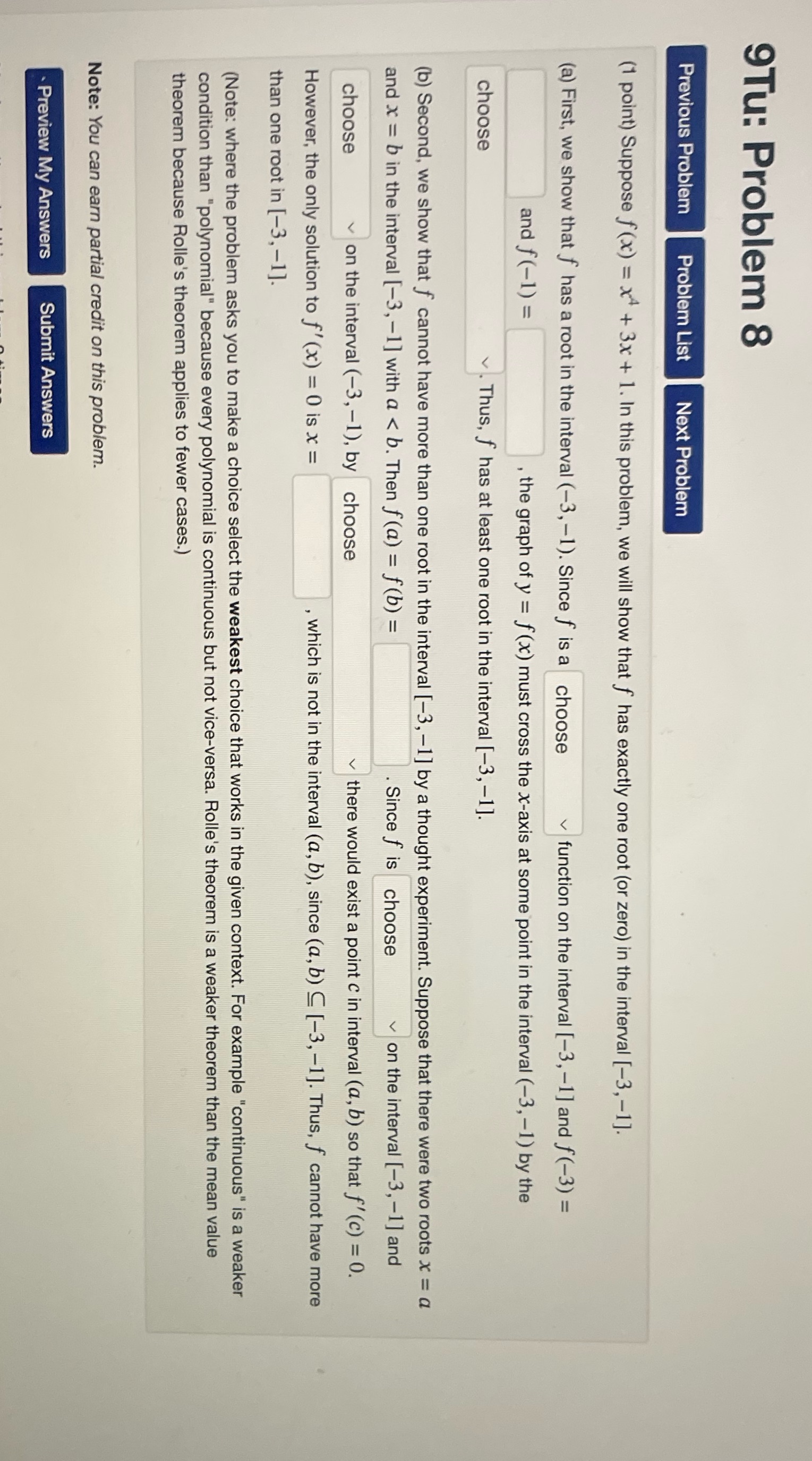
9Tu: Problem 8 Previous Problem Problem List Next Problem (1 point) Suppose f(x) = x4 + 3x + 1. In this problem, we will show that f has exactly one root (or zero) in the interval [-3, -1]. (a) First, we show that f has a root in the interval (-3, -1). Since f is a choose function on the interval [-3, -1] and f(-3) = and f (-1) = , the graph of y = f (x) must cross the x-axis at some point in the interval (-3, -1) by the choose . Thus, f has at least one root in the interval [-3, -1]. (b) Second, we show that f cannot have more than one root in the interval [-3, -1] by a thought experiment. Suppose that there were two roots x = a and x = b in the interval [-3, -1] with a