Question: (a). (5 points) Consider f(x) = tan x, for x = (-1, 1/17). Prove that f is strictly increasing. (b). (5 points) Consider its

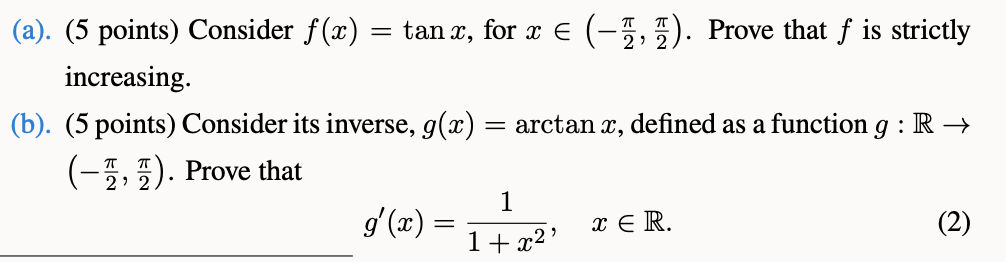
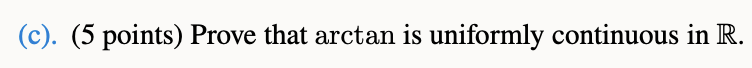
(a). (5 points) Consider f(x) = tan x, for x = (-1, 1/17). Prove that f is strictly increasing. (b). (5 points) Consider its inverse, g(x): (-). Prove that = arctan x, defined as a function 9 : R 1 g'(x) = = 1+x2' xR. (c). (5 points) Prove that arctan is uniformly continuous in R.

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

CANMNMM January of this year. (a) Each item will be held in a record. Describe all the data structures that must refer to these records to implement the required functionality. Describe all the...

In a Hopfield neural network configured as an associative memory, with all of its weights trained and fixed, what three possible behaviours may occur over time in configuration space as the net...

QUIZ... Let D be a poset and let f : D D be a monotone function. (i) Give the definition of the least pre-fixed point, fix (f), of f. Show that fix (f) is a fixed point of f. [5 marks] (ii) Show that...

Exercise Set 5.3: Graphs of the Tangent, Cotangent, Secant, and Cosecant Functions (f) Give an interval, if one exists, on which f ( x ) = tan ( x ) is increasing. Then give an Answer the following....

When it comes to journalistic endeavours or open courts, how can we best determine what personal information should be made public? In answering this question, consider how to distinguish among what...

buckley (jdb4687) - HW05 - beshaj - (53521) This print-out should have 25 questions. Multiple-choice questions may continue on the next column or page - find all choices before answering. 001...

5 page2.jpg" />9 page6.jpg" />5 page1.jpg" />5 page2.jpg" />6 page2.jpg" />5 page1.jpg" />9 page6.jpg" />9 page5.jpg" />9 page5.jpg" />9 page4.jpg" />9 page3.jpg" />8 page3.jpg" />8 page2.jpg" />8...

1. Find the domain of the function f ( x )= x 2 x +2 1) ______ (A) D=( ,2 ) ( 2, ) (B) D=( ,2 ) (2, ) (C) D= ( 2, ) (D) D=(2, ) (E) none of the above 1 2. According to the Center for Disease Control...

(a). (5 points) Consider f(x) = tanx, for x E (-?, " ). Prove that f is strictly increasing. (b). (5 points) Consider its inverse, g(x) = arctan x, defined as a function g : R -+ " ) . Prove that g'...

buckley (jdb4687) - HW06 - beshaj - (53521) This print-out should have 32 questions. Multiple-choice questions may continue on the next column or page - find all choices before answering. 001 003 2...

A small bakery produces two types of cakes: plum cake and chocolate cake. He sells plum cake for $0.69each and chocolate cake for S0.27each. If his total revenue from a day's production is $12.18,...

Guymon Solar Energy just raised (borrowed) $250 million by issuing innovative new bonds referred to as Biennial bonds. The bonds, which were issued on February 14, 2020 have a par/face value of $1000...

1 Write the correct sign, or, between each pair of fractions. They have all been started for you. a 13 b C d 40 13 8 4 4 =3. =3. 8 40 and 4-4 3 9 4-44-4 9 47 47 44 and 4-4 =-4 10 10 10 5 10

1. Suppose that the random variable X has a continuous probability density function, f(x) ={ 0, if x>0 another case calculate mean and variance. 2. Let X be a random variable with E(x) = and var(X)...

You have been just awarded the payroll contract for the company Jenns BADM50 Comprehensive Consultants (88-0000050). The company pays Bi-Monthly, with pay periods ending the 15 th and the 31 st , pay...

Is there a need for media producers to convene and discuss ways to improve their craft?

Q3. Which of the following is NOT considered as an assumption of technical analysis? a. Market value is determined solely by supply and demand. b. Supply and demand are governed by both rational and...

Different can significantly impact what a company may or may not display from its servers. a . laws regarding free speech b . national standards followed across nations C . payment mechanisms used in...

Instant coffee is made by adding boiling water (212F) to coffee mix. If the air temperature is 70F, Newtons law of cooling says that after t minutes, the temperature of the coffee will be given by a...

In Exercises 1 through 16, find the absolute maximum and absolute minimum (if any) of the given function on the specified interval. f(x) = x 3 + 3x 2 + 1; 3 x 2

Pediatricians use the formula S = 0.2029w 0.425 to estimate the surface area S (m 2 ) of a child 1 meter tall who weighs w kilograms (kg). A particular child weighs 30 kg and is gaining weight at the...

In a basketball game, the Langara College Falcons scored 54.54 % of 33 shots from the 2-point zone, 46. 6 % of 15 attempts from the 3-point distance, and 79.3% of 29 free throws (1 point each). How...

Ivory hand-soap is advertised as being 99 44/100 % pure. (It floats!) How many milligrams of impurities are in a 150-gram bar of Ivory soap?

How must you allocate your money among a number of investments so that your portfolios overall rate of return will be the same as the simple average of the rates of return on individual investments?